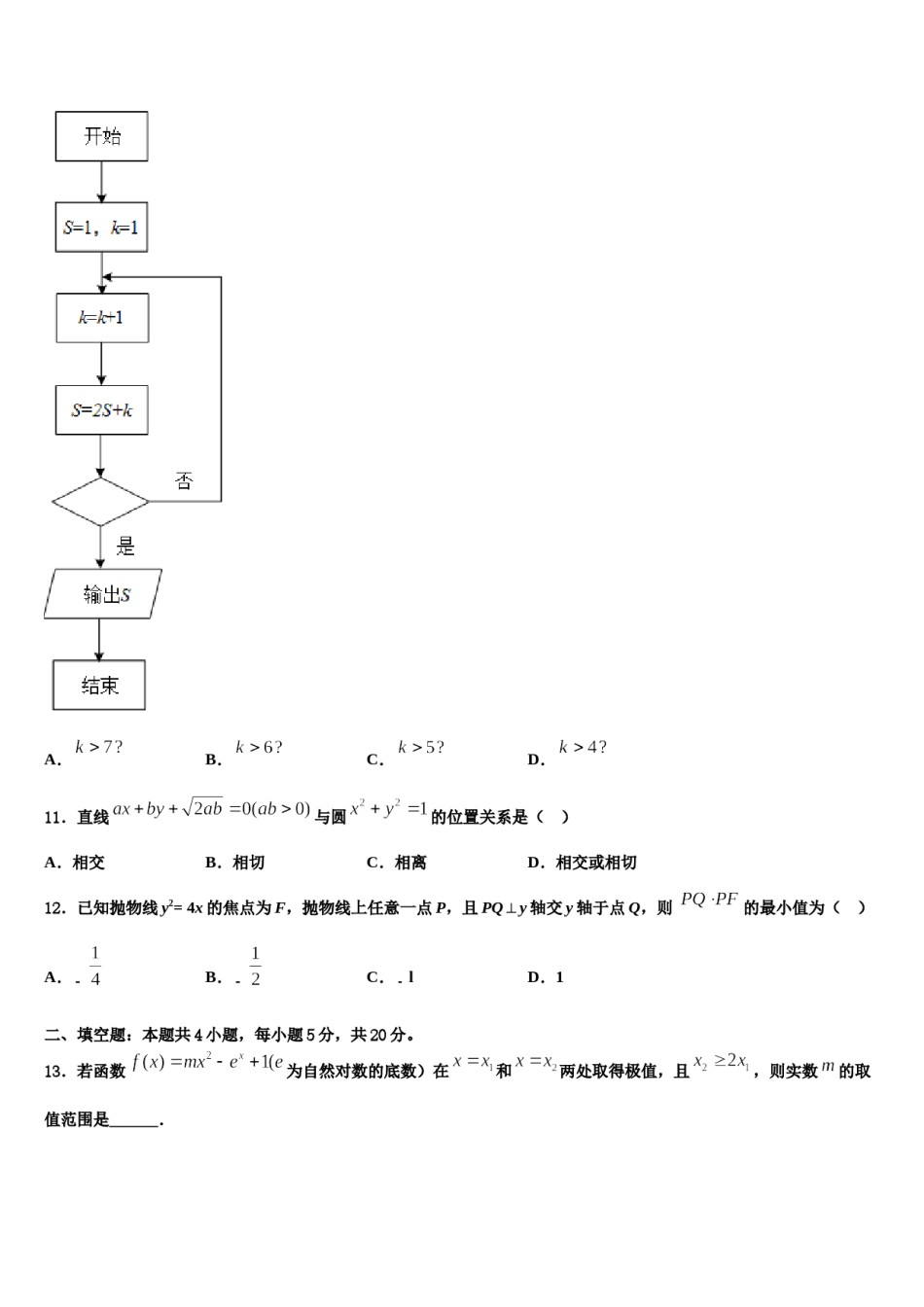
2024届广东省百校联考高三冲刺模拟数学试卷考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知椭圆的右焦点为F,左顶点为A,点P椭圆上,且,若,则椭圆的离心率为()A.B.C.D.2.已知某几何体的三视图如图所示,其中正视图与侧视图是全等的直角三角形,则该几何体的各个面中,最大面的面积为()A.2B.5C.D.3.已知点(m,8)在幂函数的图象上,设,则()A.b<a<cB.a<b<cC.b<c<aD.a<c<b4.盒中装有形状、大小完全相同的5张“刮刮卡”,其中只有2张“刮刮卡”有奖,现甲从盒中随机取出2张,则至少有一张有奖的概率为()A.B.C.D.5.如图所示,已知双曲线的右焦点为,双曲线的右支上一点,它关于原点的对称点为,满足,且,则双曲线的离心率是().A.B.C.D.6.在关于的不等式中,“”是“恒成立”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件7.若复数满足,则对应的点位于复平面的()A.第一象限B.第二象限C.第三象限D.第四象限8.函数的图象在点处的切线为,则在轴上的截距为()A.B.C.D.9.若命题:从有2件正品和2件次品的产品中任选2件得到都是正品的概率为三分之一;命题:在边长为4的正方形内任取一点,则的概率为,则下列命题是真命题的是()A.B.C.D.,则判断框内为()10.某程序框图如图所示,若输出的A.B.C.D.11.直线与圆的位置关系是()A.相交B.相切C.相离D.相交或相切12.已知抛物线y2=4x的焦点为F,抛物线上任意一点P,且PQ⊥y轴交y轴于点Q,则的最小值为(),则实数的取A.B.C.lD.1二、填空题:本题共4小题,每小题5分,共20分。13.若函数为自然对数的底数)在和两处取得极值,且值范围是______.14.已知双曲线(a>0,b>0)的两个焦点为、,点P是第一象限内双曲线上的点,且,tan∠PF2F1=﹣2,则双曲线的离心率为_____.15.已知数列为等差数列,数列为等比数列,满足,其中,,则的值为_______________.16.已知数列的前项和且,设,则的值等于_______________.(为参数).以原点O为极点,x轴三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)在平面直角坐标系xOy中,曲线C的参数方程为的正半轴为极轴,且两个坐标系取相等的长度单位,建立极坐标系.(1)设直线l的极坐标方程为,若直线l与曲线C交于两点A.B,求AB的长;(2)设M、N是曲线C上的两点,若,求面积的最大值.18.(12分)记为数列的前项和,N.(1)求;(2)令,证明数列是等比数列,并求其前项和.19.(12分)在边长为的正方形,分别为的中点,分别为的中点,现沿折叠,使三点重合,构成一个三棱锥.(1)判别与平面的位置关系,并给出证明;(2)求多面体的体积.20.(12分)选修4-5:不等式选讲已知函数的最大值为3,其中.(1)求的值;(2)若,,,求证:21.(12分)已知数列,其前项和为,若对于任意,,且,都有.,且等差数列的公差为,存在正整数,使得,(1)求证:数列是等差数列(2)若数列满足求的最小值.22.(10分)分别为的内角的对边.已知.(1)若,求;(2)已知,当的面积取得最大值时,求的周长.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、C【解析】不妨设在第一象限,故,根据得到,解得答案.【详解】不妨设在第一象限,故,,即,即,解得,(舍去).故选:.【点睛】本题考查了椭圆的离心率,意在考查学生的计算能力.2、D【解析】根据三视图还原出几何体,找到最大面,再求面积.【详解】由三视图可知,该几何体是一个三棱锥,如图所示,将其放在一个长方体中,并记为三棱锥.,,,故最大面的面积为.选D.【点睛】本题...