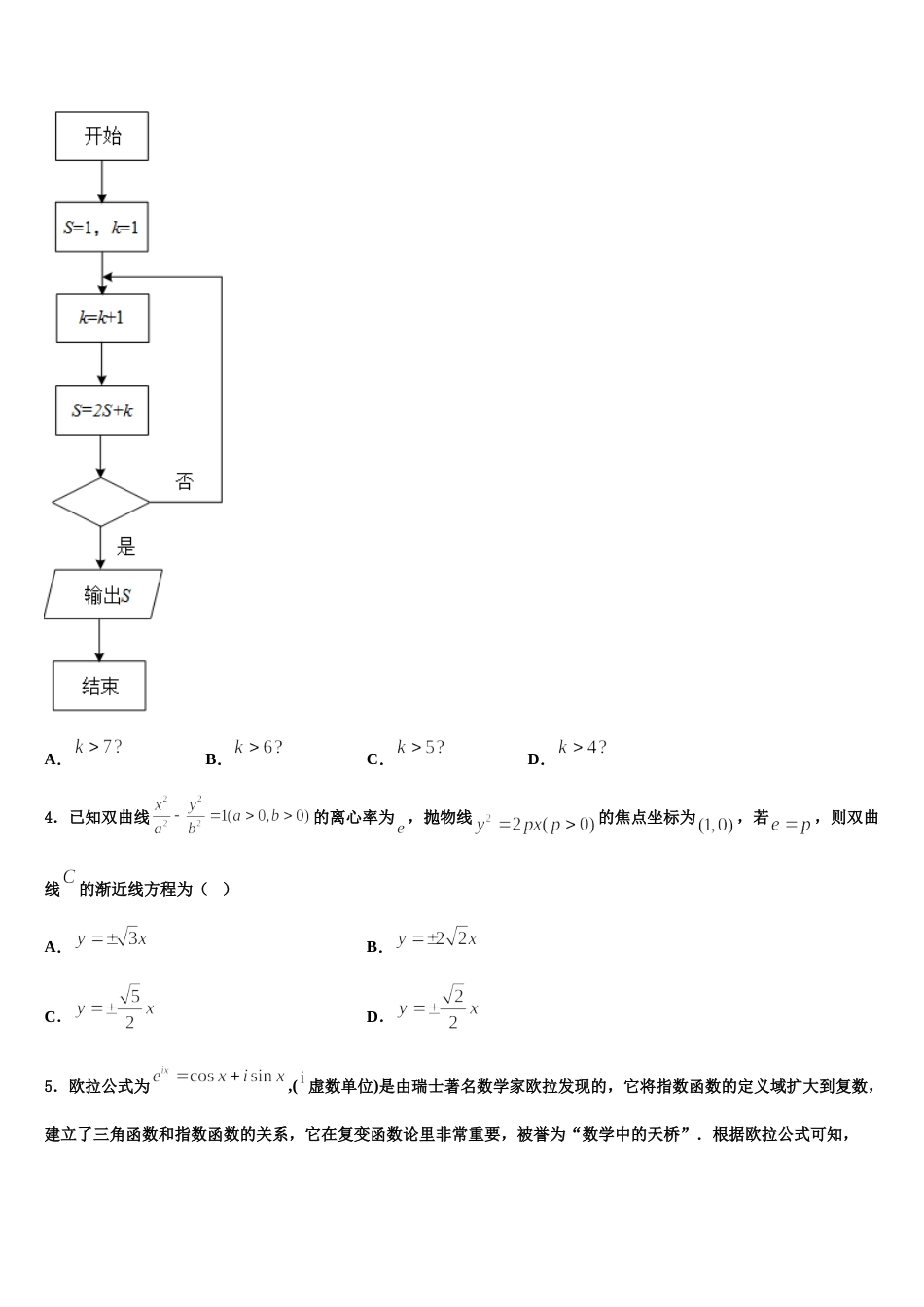
2024 届江苏省南通市实验中学高三一诊考试数学试卷请考生注意:1.请用 2B 铅笔将选择题答案涂填在答题纸相应位置上,请用 0.5 毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.过双曲线左焦点的直线 交的左支于两点,直线(是坐标原点)交的右支于点,若,且,则的离心率是( )A.B.C.D.2.若双曲线的一条渐近线与直线垂直,则该双曲线的离心率为( )A.2B.C.D.3.某程序框图如图所示,若输出的,则判断框内为( )A.B.C.D.4.已知双曲线的离心率为 ,抛物线的焦点坐标为,若,则双曲线的渐近线方程为( )A.B.C.D.5.欧拉公式为,( 虚数单位)是由瑞士著名数学家欧拉发现的,它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里非常重要,被誉为“数学中的天桥”.根据欧拉公式可知,表示的复数位于复平面中的( )A.第一象限B.第二象限C.第三象限D.第四象限6.已知等比数列的前项和为,且满足,则的值是( )A.B.C.D.7.在中,角、 、 的对边分别为、 、 ,若,,,则( )A.B.C.D.8.波罗尼斯(古希腊数学家,的公元前 262-190 年)的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽,几乎使后人没有插足的余地.他证明过这样一个命题:平面内与两定点距离的比为常数 k(k>0,且 k≠1)的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.现有椭圆=1(a>b>0),A,B 为椭圆的长轴端点,C,D 为椭圆的短轴端点,动点 M 满足=2,△MAB 面积的最大值为 8,△MCD 面积的最小值为1,则椭圆的离心率为( )A.B.C.D.9.在中,点为中点,过点的直线与,所在直线分别交于点,,若,,则的最小值为( )A.B.2C.3D.10.下图是来自古希腊数学家希波克拉底所研究的几何图形,此图由三个半圆构成,三个半圆的直径分别为直角三角形的斜边、直角边,已知以直角边为直径的半圆的面积之比为,记,则( )A.B.C.1D.11.过双曲线的右焦点 F 作双曲线 C 的一条弦 AB,且,若以 AB 为直径的圆经过双曲线 C 的左顶点,则双曲线 C 的离心率为( )A.B.C.2D.12.已知集合,则元素个数为( )A.1B.2C.3D.4二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.若双曲线 C:(,)的顶点到渐近线的距离为,则的最小值________.14.已知的展开式中第项与第项的二项式系数相等,则__________.15.已知数列满足,则________.16.已知向量,且,则___________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知为坐标原点,单位圆与角终边的交点为,过作平行于轴的直线 ,设 与终边所在直线的交点为,.(1)求函数的最小正周期;(2)求函数在区间上的值域.18.(12 分)某网络商城在年 月 日开展“庆元旦”活动,当天各店铺销售额破十亿,为了提高各店铺销售的积极性,采用摇号抽奖的方式,抽取了家店铺进行红包奖励.如图是抽取的家店铺元旦当天的销售额(单位:千元)的频率分布直方图.(1)求抽取的这家店铺,元旦当天销售额的平均值;(2)估计抽取的家店铺中元旦当天销售额不低于元的有多少家;(3)为了了解抽取的各店铺的销售方案,销售额在和的店铺中共抽取两家店铺进行销售研究,求抽取的店铺销售额在中的个数的分布列和数学期望.19.(12 分)已知函数.(1)若在上是减函数,求实数的最大值;(2)若,求证:.20.(12 分)已知椭圆的右焦点为,直线被称作为椭圆的一条准线,点在椭圆上(异于椭圆左、右顶点),过点作直线与椭圆相切,且与直线 相交于点.(1)求证:.(2)若点在轴的上方,当的面积最小时,求直线的斜率.附:多项式因式分解公式:21.(12 分)已知在等比数列中,.(1)求数列的通项公式;(2)若,求数列前项的和.22.(10 分)已...