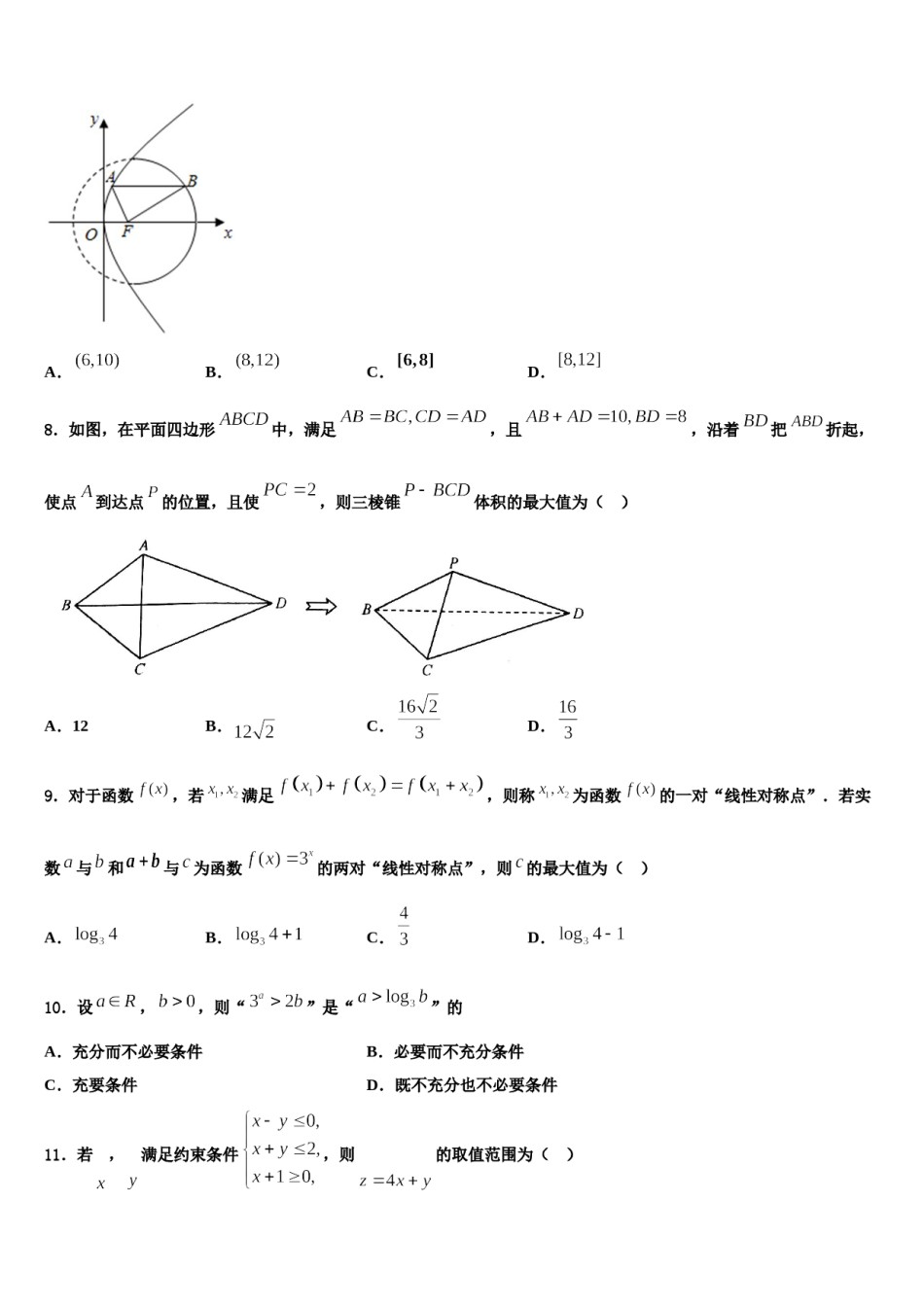
2024届江苏省常州市教育学会学业水平监测高考数学考前最后一卷预测卷注意事项:1.答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.函数的部分图象如图所示,已知,函数的图象可由图象向右平移个单位长度而得到,则函数的解析式为()A.B.C.D.2.“”是“,”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件3.已知抛物线:,直线与分别相交于点,与的准线相交于点,若,则()A.3B.C.D.4.如图,四边形为正方形,延长至,使得,点在线段上运动.设,则的取值范围是()A.B.C.D.5.下列命题为真命题的个数是()(其中,为无理数)①;②;③.A.0B.1C.2D.36.我国古代数学巨著《九章算术》中,有如下问题:“今有女子善织,日自倍,五日织五尺,问日织几何?”这个问题用今天的白话叙述为:有一位善于织布的女子,每天织的布都是前一天的2倍,已知她5天共织布5尺,问这位女子每天分别织布多少?根据上述问题的已知条件,若该女子共织布尺,则这位女子织布的天数是()A.2B.3C.4D.17.如图所示点是抛物线的焦点,点、分别在抛物线及圆的实线部分上运动,且总是平行于轴,则的周长的取值范围是()A.B.C.D.,且8.如图,在平面四边形中,满足,沿着把折起,使点到达点的位置,且使,则三棱锥体积的最大值为()A.12B.C.D.9.对于函数,若满足,则称为函数的一对“线性对称点”.若实数与和与为函数的两对“线性对称点”,则的最大值为()A.B.C.D.10.设,,则“”是“”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件11.若,满足约束条件,则的取值范围为()A.B.C.D.12.已知集合A,B=,则A∩B=A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.将2个相同的红球和2个相同的黑球全部放入甲、乙、丙、丁四个盒子里,其中甲、乙盒子均最多可放入2个球,丙、丁盒子均最多可放入1个球,且不同颜色的球不能放入同一个盒子里,共有________种不同的放法.14.设数列的前项和为,且对任意正整数,都有,则___15.已知复数(为虚数单位),则的共轭复数是_____,_____.16.若函数满足:①是偶函数;②的图象关于点对称.则同时满足①②的,的一组值可以分别是__________.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知向量,.(1)求的最小正周期;(2)若的内角的对边分别为,且,求的面积.18.(12分)已知椭圆与x轴负半轴交于,离心率.(1)求椭圆C的方程;(2)设直线与椭圆C交于两点,连接AM,AN并延长交直线x=4于两点,若,直线MN是否恒过定点,如果是,请求出定点坐标,如果不是,请说明理由.19.(12分)如图,四棱锥,侧面是边长为2的正三角形,且与底面垂直,底面是的菱形,为棱上的动点,且.的平面角余弦值为.(I)求证:为直角三角形;(II)试确定的值,使得二面角20.(12分)如图,三棱锥中,(1)证明:面面;(2)求二面角的余弦值.21.(12分)设函数,.(Ⅰ)讨论的单调性;(Ⅱ)时,若,,求证:..22.(10分)已知;(1)若为真命题,求实数的取值范围;的取值范围.(2)若为真命题且为假命题,求实数参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、A【解析】由图根据三角函数图像的对称性可得,利用周期公式可得,再根据图像过,即可求出,再利用三角函数的平移变换即可求解.【详解】由图像可知,即,所以,解得,又,所以,由,所以或,又,所以,,所以,,即,因为函数的图象由图象向右平移个单位长度而得到,所以.故...