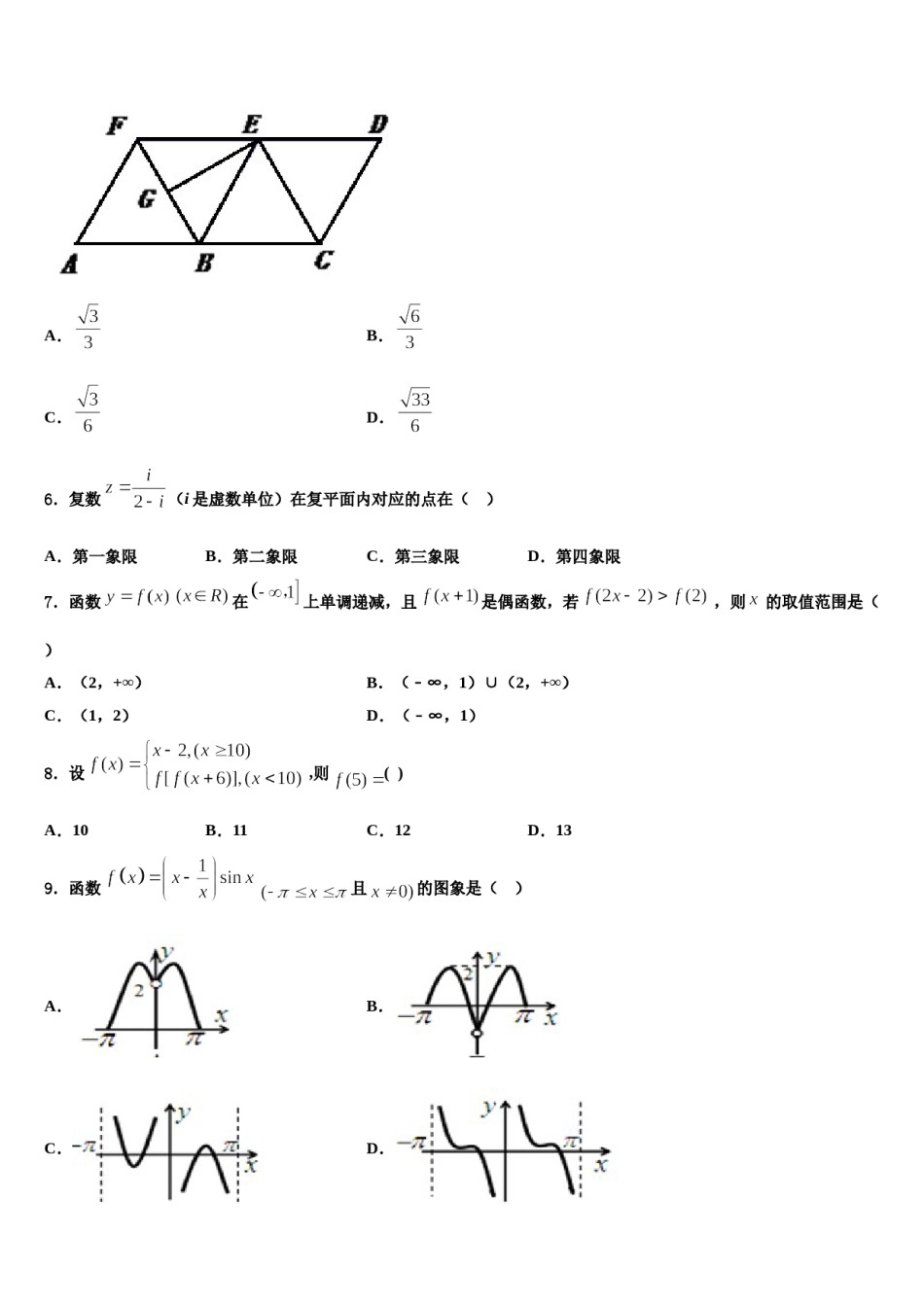
2024届河北省滁州市衡水中学高三下学期一模考试数学试题请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.命题“”的否定是()A.B.C.D.2.已知双曲线与双曲线有相同的渐近线,则双曲线的离心率为()A.B.C.D.3.已知向量,,且,则()A.B.C.1D.24.已知实数满足不等式组,则的最小值为()A.B.C.D.5.下图为一个正四面体的侧面展开图,为的中点,则在原正四面体中,直线与直线所成角的余弦值为()A.B.C.D.6.复数(i是虚数单位)在复平面内对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限7.函数在上单调递减,且是偶函数,若,则的取值范围是()B.(﹣∞,1)∪(2,+∞)A.(2,+∞)D.(﹣∞,1)C.(1,2)8.设,则()A.10B.11C.12D.139.函数且的图象是()A.B.C.D.10.已知函数,若恒成立,则满足条件的的个数为()A.0B.1C.2D.311.已知集合,B={y∈Ny=x﹣1,x∈A},则A∪B=()A.{﹣1,0,1,2,3}B.{﹣1,0,1,2}C.{0,1,2}D.{x﹣1≤x≤2}12.已知函数是奇函数,且,若对,恒成立,则的取值范围是()A.B.C.D.的值为_____.二、填空题:本题共4小题,每小题5分,共20分。13.如图,在平行四边形中,,,则14.已知以x±2y=0为渐近线的双曲线经过点,则该双曲线的标准方程为________.15.若函数,则使得不等式成立的的取值范围为_________.16.已知函数,则函数的极大值为___________.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)如图,设A是由个实数组成的n行n列的数表,其中aij(i,j=1,2,3,…,n)表示位于第i行第j列的实数,且aij{1,-1}.记S(n,n)为所有这样的数表构成的集合.对于,记ri(A)为A的第i行各数之积,cj(A)为A的第j列各数之积.令a11a12…a1na21a22a2n…………an1an2…ann(Ⅰ)请写出一个AS(4,4),使得l(A)=0;(Ⅱ)是否存在AS(9,9),使得l(A)=0?说明理由;(Ⅲ)给定正整数n,对于所有的AS(n,n),求l(A)的取值集合.18.(12分)在中,角,,的对边分别为,,,,.,且的面积为.(1)求;(2)求的周长.19.(12分)已知函数(Ⅰ)若,求曲线在点处的切线方程;(Ⅱ)若在上恒成立,求实数的取值范围;(Ⅲ)若数列的前项和,,求证:数列的前项和20.(12分)如图,在直角中,,,,点在线段上.(1)若,求的长;(2)点是线段上一点,,且,求的值.21.(12分)已知函数.(1)讨论的单调性并指出相应单调区间;(2)若,设是函数的两个极值点,若,且恒成立,求实数k的取值范围.22.(10分)在直角坐标系中,直线的参数方程为(为参数),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为,点的极坐标为.(1)求的直角坐标方程和的直角坐标;(2)设与交于,两点,线段的中点为,求.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、D【解析】根据全称命题的否定是特称命题,对命题进行改写即可.【详解】全称命题的否定是特称命题,所以命题“,”的否定是:,.故选D.【点睛】本题考查全称命题的否定,难度容易.2、C【解析】由双曲线与双曲线有相同的渐近线,列出方程求出的值,即可求解双曲线的离心率,得到答案.【详解】由双曲线与双曲线有相同的渐近线,可得,解得,此时双曲线,则曲线的离心率为,故选C.【点睛】本题主要考查了双曲线的标准方程及其简单的几何性质的应用,其中解答中熟记双曲线的几何性质,准确运算是解答的关键,着重考查了运算与求解能力,属于基础题.3、A【解析】根据向量垂直的坐标表示列方程,解方程求得的值.【详解】由于向量,,且,所以解得.故选:A【点睛】本小题主要考查向量垂直的坐标表示,属于基础题.4、B【解析】作出约束...