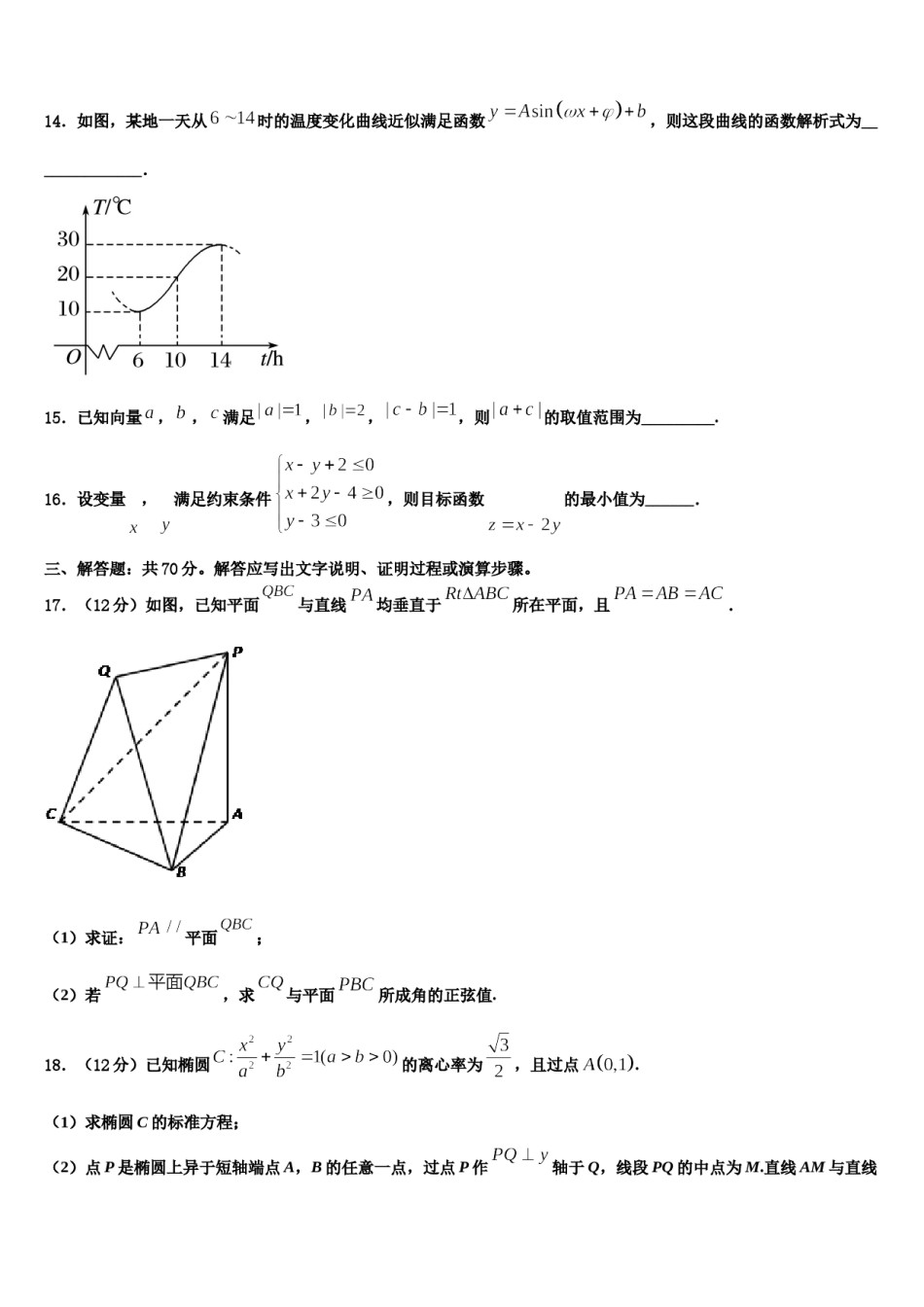
2024届河南省安阳市林州市林州一中高考数学押题试卷请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知,,,则()A.B.C.D.2.已知平面向量,,,则实数x的值等于()A.6B.1C.D.3.设平面与平面相交于直线,直线在平面内,直线在平面内,且则“”是“”的()B.必要不充分条件A.充分不必要条件D.即不充分不必要条件C.充要条件4.向量,,且,则()A.B.C.D.5.将函数的图象分别向右平移个单位长度与向左平移(>0)个单位长度,若所得到的两个图象重合,则的最小值为()A.B.C.D.6.已知函数,若则()A.f(a)<f(b)<f(c)B.f(b)<f(c)<f(a)C.f(a)<f(c)<f(b)D.f(c)<f(b)<f(a)7.已知,,分别为内角,,的对边,,,的面积为,则()A.B.4C.5D.8.若的展开式中的系数为150,则()A.20B.15C.10D.259.已知l,m是两条不同的直线,m⊥平面α,则“”是“l⊥m”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件10.马林●梅森是17世纪法国著名的数学家和修道士,也是当时欧洲科学界一位独特的中心人物,梅森在欧几里得、费马等人研究的基础上对2p﹣1作了大量的计算、验证工作,人们为了纪念梅森在数论方面的这一贡献,将形如2P﹣1(其中p是素数)的素数,称为梅森素数.若执行如图所示的程序框图,则输出的梅森素数的个数是()A.3B.4C.5D.611.设,集合,则()A.B.C.D.12.已知集合A={yy=x﹣1,x∈R},B={xx≥2},则下列结论正确的是()A.﹣3∈AB.3BC.A∩B=BD.A∪B=B二、填空题:本题共4小题,每小题5分,共20分。13.已知函数恰好有3个不同的零点,则实数的取值范围为____14.如图,某地一天从时的温度变化曲线近似满足函数,则这段曲线的函数解析式为______________.15.已知向量,,满足,,,则的取值范围为_________.16.设变量,满足约束条件,则目标函数的最小值为______.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)如图,已知平面与直线均垂直于所在平面,且.(1)求证:平面;所成角的正弦值.(2)若,求与平面18.(12分)已知椭圆的离心率为,且过点.(1)求椭圆C的标准方程;轴于Q,线段PQ的中点为M.直线AM与直线(2)点P是椭圆上异于短轴端点A,B的任意一点,过点P作交于点N,D为线段BN的中点,设O为坐标原点,试判断以OD为直径的圆与点M的位置关系.19.(12分)已知椭圆()的半焦距为,原点到经过两点,的直线的距离为.的一条直径,若椭圆经过,两点,求椭圆的方程.(Ⅰ)求椭圆的离心率;(Ⅱ)如图,是圆20.(12分)如图,底面是等腰梯形,,点为的中点,以为边作正方形,且平面平面.(1)证明:平面平面.(2)求二面角的正弦值.21.(12分)已知函数(1)若函数在处取得极值1,证明:(2)若恒成立,求实数的取值范围.22.(10分)已知函数.的值域.(1)当时,求函数(2)设函数,若,且的最小值为,求实数的取值范围.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、B【解析】利用指数函数和对数函数的单调性,将数据和做对比,即可判断.【详解】由于,,故.故选:B.【点睛】本题考查利用指数函数和对数函数的单调性比较大小,属基础题.2、A【解析】根据向量平行的坐标表示即可求解.【详解】,,,,即,故选:A【点睛】本题主要考查了向量平行的坐标运算,属于容易题.3、A【解析】试题分析:α⊥β,b⊥m又直线a在平面α内,所以a⊥b,但直线不一定相交,所以“α⊥β”是“a⊥b”的充分不必要条件,故选A.考点:充分条件、必要条件.4、D【解析】根据向量平行的坐标运算以及诱导公式,即可得出答案.【详解】故选:D【点睛】本题主要考查了由向量平行求参数以及诱导公式的应用,属...