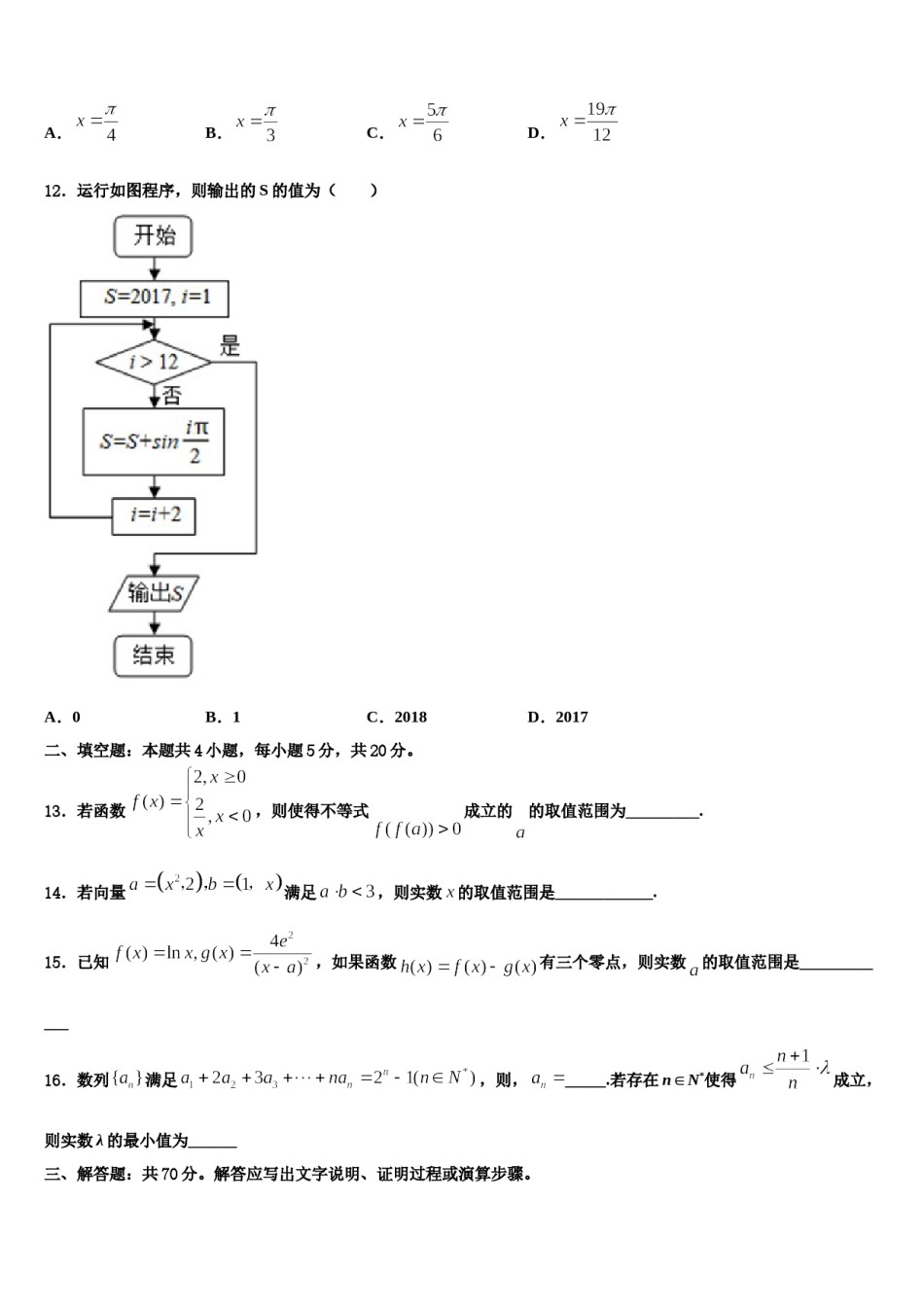
2024届浙江省温州市重点中学高三第三次测评数学试卷请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知双曲线的左、右顶点分别是,双曲线的右焦点为,点在过且垂直于轴的直线上,当的外接圆面积达到最小时,点恰好在双曲线上,则该双曲线的方程为()A.B.C.D.2.已知直线:()与抛物线:交于(坐标原点),两点,直线:与抛物线交于,两点.若,则实数的值为()A.B.C.D.3.已知曲线且过定点,若且,则的最小值为().A.B.9C.5D.4.已知复数在复平面内对应的点的坐标为,则下列结论正确的是()A.B.复数的共轭复数是C.D.5.已知点P不在直线l、m上,则“过点P可以作无数个平面,使得直线l、m都与这些平面平行”是“直线l、m互相平行”的()B.必要不充分条件A.充分不必要条件D.既不充分也不必要条件C.充分必要条件6.已知各项都为正的等差数列中,,若,,成等比数列,则(),记,PO,A.B.C.D.7.已知P是双曲线渐近线上一点,,是双曲线的左、右焦点,的斜率为,k,,若,-2k,成等差数列,则此双曲线的离心率为()A.B.C.D.8.设F为双曲线C:(a>0,b>0)的右焦点,O为坐标原点,以OF为直径的圆与圆x2+y2=a2交于P、Q两点.若PQ=OF,则C的离心率为A.B.C.2D.9.记集合和集合表示的平面区域分别是和,若在区域内任取一点,则该点落在区域的概率为()A.B.C.D.10.已知复数,则的虚部为()A.-111.函数B.C.1D.对称轴是()的最小正周期是,则其图象向左平移个单位长度后得到的函数的一条A.B.C.D.12.运行如图程序,则输出的S的值为()A.0B.1C.2018D.2017二、填空题:本题共4小题,每小题5分,共20分。13.若函数,则使得不等式成立的的取值范围为_________.14.若向量满足,则实数的取值范围是____________.15.已知,如果函数有三个零点,则实数的取值范围是____________16.数列满足,则,_____.若存在n∈N使得成立,则实数λ的最小值为______三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)如图中,为的中点,,,.(1)求边的长;的角平分线,求的面积.(2)点在边上,若是18.(12分)已知函数.(1)讨论的单调性;(2)函数,若对于,使得成立,求的取值范围.19.(12分)已知实数x,y,z满足,证明:.20.(12分)已知函数.(1)当时,求函数的值域;(2)的角的对边分别为且,,求边上的高的最大值.21.(12分)如图,在矩形中,,,点是边上一点,且,点是的中点,将沿着折起,使点运动到点处,且满足.(1)证明:平面;(2)求二面角的余弦值.22.(10分)随着电子阅读的普及,传统纸质媒体遭受到了强烈的冲击.某杂志社近9年来的纸质广告收入如下表所示:根据这9年的数据,对和作线性相关性检验,求得样本相关系数的绝对值为0.243;根据后5年的数据,对和作线性相关性检验,求得样本相关系数的绝对值为0.984.(1)如果要用线性回归方程预测该杂志社2019年的纸质广告收入,现在有两个方案,方案一:选取这9年数据进行预测,方案二:选取后5年数据进行预测.从实际生活背景以及线性相关性检验的角度分析,你觉得哪个方案更合适?附:相关性检验的临界值表:(2)某购物网站同时销售某本畅销书籍的纸质版本和电子书,据统计,在该网站购买该书籍的大量读者中,只购买电子书的读者比例为,纸质版本和电子书同时购买的读者比例为,现用此统计结果作为概率,若从上述读者中随机调查了3位,求购买电子书人数多于只购买纸质版本人数的概率.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、A【解析】点的坐标为,,展开利用均值不等式得到最值,将点代入双曲线计算得到答案.,由于为定值,由正弦定理可知当取得最大值时,的外接【详解...