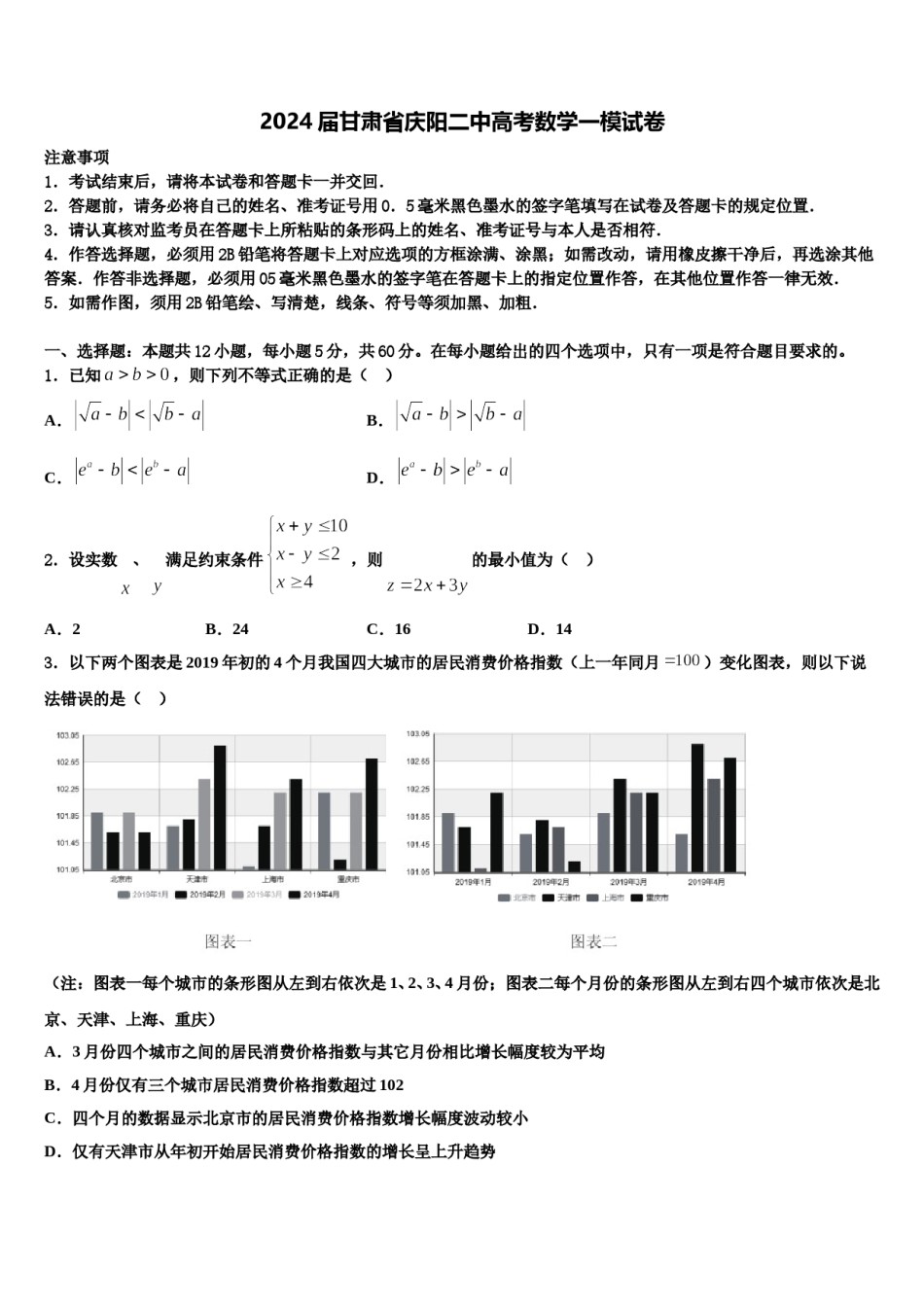
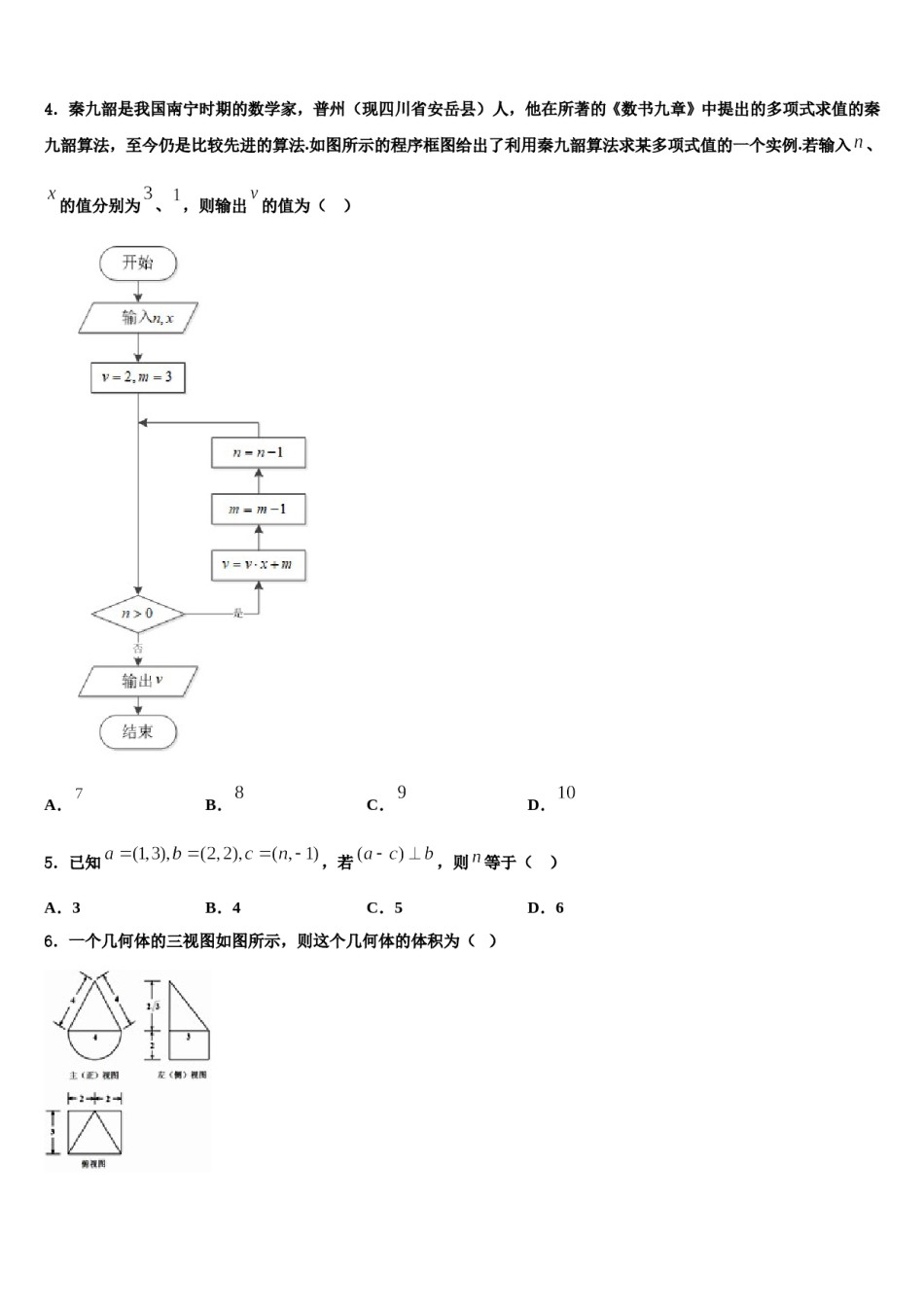
2024届甘肃省庆阳二中高考数学一模试卷注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知,则下列不等式正确的是()A.B.C.D.2.设实数、满足约束条件,则的最小值为()A.2B.24C.16D.143.以下两个图表是2019年初的4个月我国四大城市的居民消费价格指数(上一年同月)变化图表,则以下说法错误的是()(注:图表一每个城市的条形图从左到右依次是1、2、3、4月份;图表二每个月份的条形图从左到右四个城市依次是北京、天津、上海、重庆)A.3月份四个城市之间的居民消费价格指数与其它月份相比增长幅度较为平均B.4月份仅有三个城市居民消费价格指数超过102C.四个月的数据显示北京市的居民消费价格指数增长幅度波动较小D.仅有天津市从年初开始居民消费价格指数的增长呈上升趋势4.秦九韶是我国南宁时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例.若输入、的值分别为、,则输出的值为()A.B.C.D.5.已知,若,则等于()A.3B.4C.5D.66.一个几何体的三视图如图所示,则这个几何体的体积为()A.B.C.D.7.甲乙两人有三个不同的学习小组,,可以参加,若每人必须参加并且仅能参加一个学习小组,则两人参加同一个小组的概率为()A.B.C.D.8.已知函数若关于的方程有六个不相等的实数根,则实数的C.D.取值范围为()A.B.9.已知随机变量X的分布列如下表:X01Pabc其中a,b,.若X的方差对所有都成立,则()A.B.C.D.10.某四棱锥的三视图如图所示,则该四棱锥的表面积为()A.8B.C.D.11.已知实数集,集合,集合,则()A.B.C.D.12.已知数列为等差数列,为其前项和,,则()D.84A.7B.14C.28二、填空题:本题共4小题,每小题5分,共20分。13.设函数,当时,记最大值为,则的最小值为______.14.在平面直角坐标系中,已知点,,若圆上有且仅有一对点,使得的面积是的面积的2倍,则的值为_______.15.若正三棱柱的所有棱长均为2,点为侧棱上任意一点,则四棱锥的体积为__________.16.已知数列与均为等差数列(),且,则______.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)在直角坐标系中,已知直线的直角坐标方程为,曲线的参数方程为(为参数),以直角坐标系原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为.(1)求曲线和直线的极坐标方程;(2)已知直线与曲线、相交于异于极点的点,若的极径分别为,求的值.18.(12分)在平面直角坐标系中,,,且满足(1)求点的轨迹的方程;(2)过,作直线交轨迹于,两点,若的面积是面积的2倍,求直线的方.程.19.(12分)已知函数(1)求不等式的解集;(2)若函数的最大值为,且,求的最小值.20.(12分)设的解集;(1)当时,求不等式(2)若,求的取值范围.21.(12分)某精密仪器生产车间每天生产个零件,质检员小张每天都会随机地从中抽取50个零件进行检查是否合格,若较多零件不合格,则需对其余所有零件进行检查.根据多年的生产数据和经验,这些零件的长度服从正态分布(单位:微米),且相互独立.若零件的长度满足,则认为该零件是合格的,否则该零件不合格.及的数学期望;(1)假设某一天小张抽查出不合格的零件数为,求(2)小张某天恰好从50个零件中检查出2个不合格的零件,若以此频率作为当天生产零件...