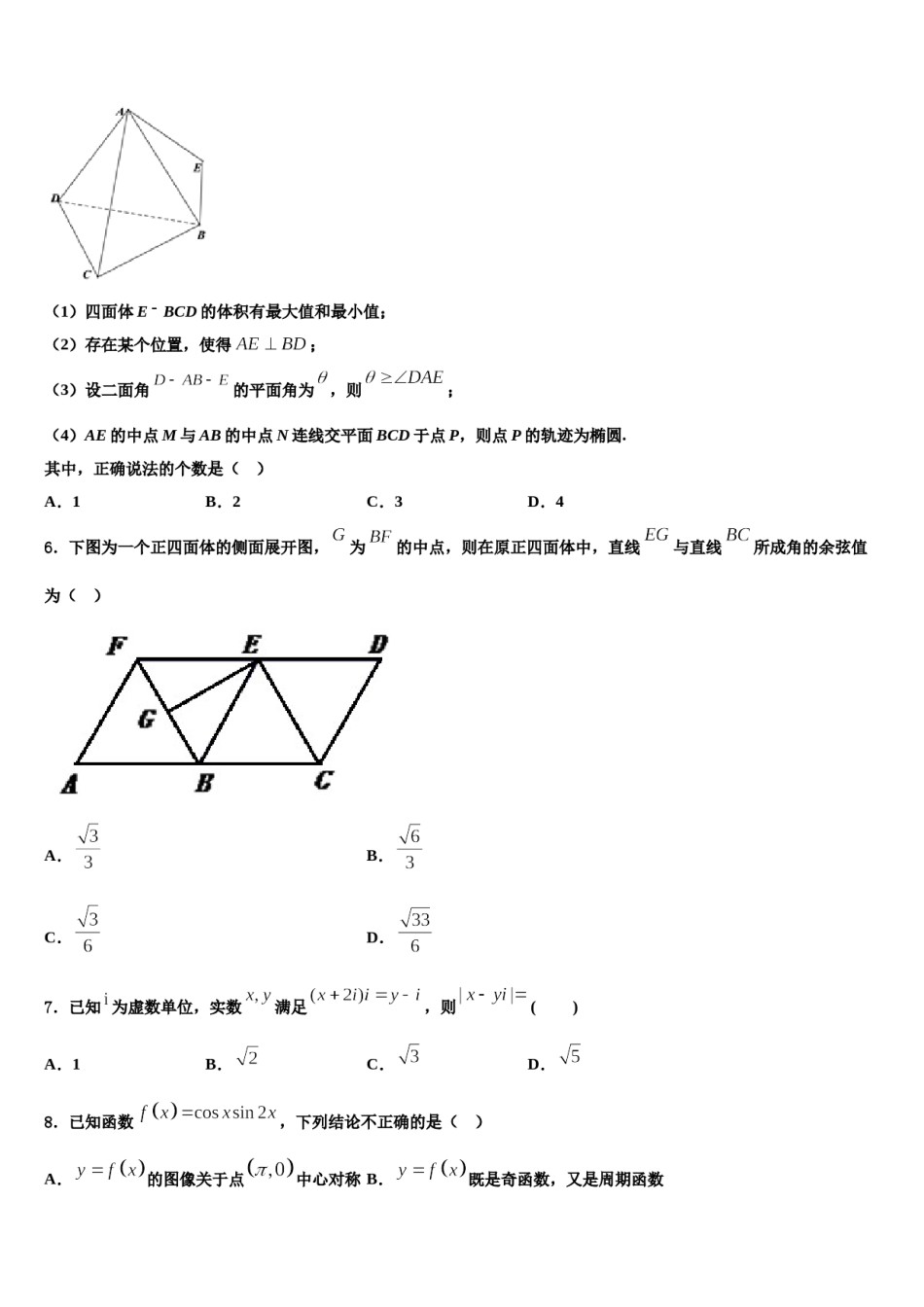
2024届甘肃省玉门市玉门一中高考仿真卷数学试卷请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知实数满足约束条件,则的最小值为()A.-5B.2C.7D.112.已知,,,,.若实数,满足不等式组,则目标函数()B.有最大值,有最小值A.有最大值,无最小值D.无最大值,无最小值C.无最大值,有最小值3.已知复数满足,其中为虚数单位,则().A.B.C.D.4.设是定义在实数集上的函数,满足条件是偶函数,且当时,,则,,的大小关系是()A.B.C.D.侧棱,直角边AE绕斜边AB旋转,则在旋转的过程中,有下5.等腰直角三角形的斜边AB为正四面体列说法:(1)四面体EBCD的体积有最大值和最小值;(2)存在某个位置,使得;(3)设二面角的平面角为,则;(4)AE的中点M与AB的中点N连线交平面BCD于点P,则点P的轨迹为椭圆.其中,正确说法的个数是()A.1B.2C.3D.46.下图为一个正四面体的侧面展开图,为的中点,则在原正四面体中,直线与直线所成角的余弦值为()A.B.C.D.7.已知为虚数单位,实数满足,则()A.1B.C.D.8.已知函数,下列结论不正确的是()A.的图像关于点中心对称B.既是奇函数,又是周期函数C.的图像关于直线对称D.的最大值是9.若,,,则下列结论正确的是()A.B.C.D.10.已知函数,对任意的,,当时,,则下列判断正确的是()A.B.函数在上递增C.函数的一条对称轴是D.函数的一个对称中心是11.若关于的不等式有正整数解,则实数的最小值为()A.B.C.D.12.设点,,不共线,则“”是“”()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分又不必要条件二、填空题:本题共4小题,每小题5分,共20分。13.若,则__________.14.从编号为,,,的张卡片中随机抽取一张,放回后再随机抽取一张,则第二次抽得的卡片上的数字能被第一次抽得的卡片上数字整除的概率为_____________.15.已知,分别是椭圆:()的左、右焦点,过左焦点的直线与椭圆交于、两点,且,,则椭圆的离心率为__________.16.(5分)有一道描述有关等差与等比数列的问题:有四个和尚在做法事之前按身高从低到高站成一列,已知前三个和尚的身高依次成等差数列,后三个和尚的身高依次成等比数列,且前三个和尚的身高之和为cm,中间两个和尚的身高之和为cm,则最高的和尚的身高是____________cm.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知向量,函数.(1)求函数的最小正周期及单调递增区间;(2)在中,三内角的对边分别为,已知函数的图像经过点,成等差数列,且,求a的值.18.(12分)设函数.(1)当时,求不等式的解集;(2)当时,求实数的取值范围.19.(12分)追求人类与生存环境的和谐发展是中国特色社会主义生态文明的价值取向.为了改善空气质量,某城市环保局随机抽取了一年内100天的空气质量指数(AQI)的检测数据,结果统计如表:AQI空气质量优良轻度污染中度污染重度污染重度污染天数61418272510(1)从空气质量指数属于[0,50],(50,100]的天数中任取3天,求这3天中空气质量至少有2天为优的概率;(2)已知某企业每天因空气质量造成的经济损失y(单位:元)与空气质量指数x的关系式为,假设该企业所在地7月与8月每天空气质量为优、良、轻度污染、中度污染、重度污染、严重污染的概率分别为.9月每天的空气质量对应的概率以表中100天的空气质量的频率代替.(i)记该企业9月每天因空气质量造成的经济损失为X元,求X的分布列;(ii)试问该企业7月、8月、9月这三个月因空气质量造成的经济损失总额的数学期望是否会超过2.88万元?说明你的理由.20.(12分)设函数,().(1)若曲线在点处的切线方程为,求实数a、m的值;(2)若对任意恒成立,求实数a的取值范围;(3)关于x的方程能否有三个不同的实...