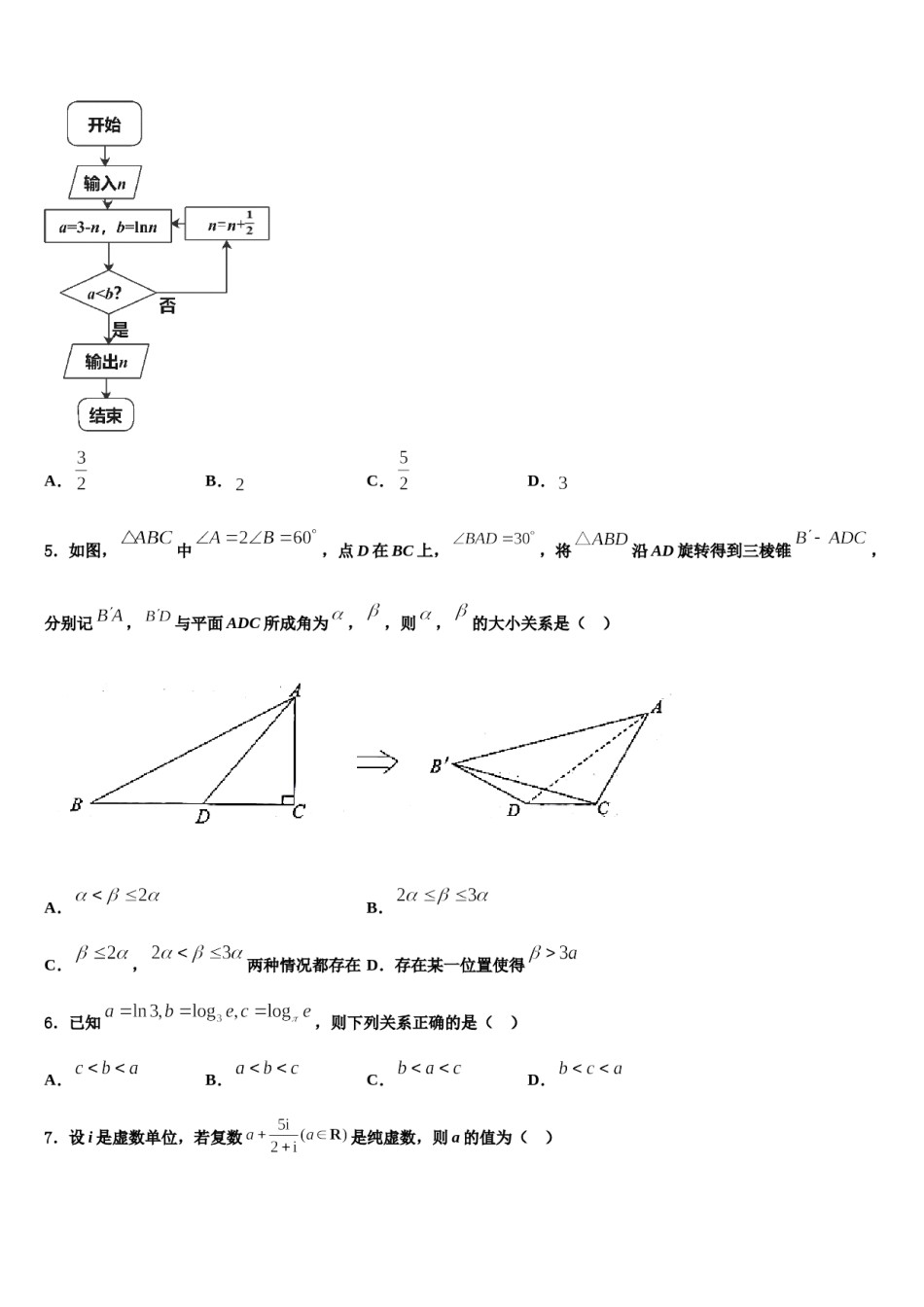
2024届甘肃省白银市靖远县第四中学高三第二次联考数学试卷注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.某三棱锥的三视图如图所示,网格纸上小正方形的边长为,则该三棱锥外接球的表面积为()A.B.C.D.2.已知函数,若,且,则的取值范围为()A.B.C.D.3.已知抛物线上一点的纵坐标为4,则点到抛物线焦点的距离为()A.2B.3C.4D.54.执行如图所示的程序框图若输入,则输出的的值为()A.B.C.D.5.如图,中,点D在BC上,,将沿AD旋转得到三棱锥,分别记,与平面ADC所成角为,,则,的大小关系是()A.B.C.,两种情况都存在D.存在某一位置使得6.已知,则下列关系正确的是()A.B.C.D.7.设i是虚数单位,若复数是纯虚数,则a的值为()A.B.3C.1D.8.设椭圆:的右顶点为A,右焦点为F,B、C为椭圆上关于原点对称的两点,直线BF交直线AC于M,且M为AC的中点,则椭圆E的离心率是()A.B.C.D.9.已知双曲线的一条渐近线与直线垂直,则双曲线的离心率等于()A.B.C.D.的左右焦点分别为10.已知双曲线,,以线段为直径的圆与双曲线在第二象限的交点为,若直线与圆相切,则双曲线的渐近线方程是()D.A.B.C.,则双曲线的离心率为()11.已知双曲线的一条渐近线方程为A.B.C.D.12.已知函数的导函数为,记,,…,N.若,则()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.关于函数有下列四个命题:①函数在上是增函数;②函数的图象关于中心对称;③不存在斜率小于且与函数的图象相切的直线;④函数的导函数不存在极小值.其中正确的命题有______.(写出所有正确命题的序号)14.已知是第二象限角,且,,则____.15.在编号为1,2,3,4,5且大小和形状均相同的五张卡片中,一次随机抽取其中的三张,则抽取的三张卡片编号之和是偶数的概率为________.16.函数的值域为_________.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)在直角坐标系中,曲线的参数方程为(为参数,将曲线经过伸缩变换后得到曲线.在以原点为极点,轴正半轴为极轴的极坐标系中,直线的极坐标方程为.(1)说明曲线是哪一种曲线,并将曲线的方程化为极坐标方程;(2)已知点是曲线上的任意一点,又直线上有两点和,且,又点的极角为,点的极角为锐角.求:①点的极角;②面积的取值范围.18.(12分)设数列的前列项和为,已知.(1)求数列的通项公式;(2)求证:.19.(12分)已知函数,.(1)求证:在区间上有且仅有一个零点,且;(2)若当时,不等式恒成立,求证:.20.(12分)已知数列满足,.(1)求数列的通项公式;(2)若,求数列的前项和.21.(12分)在中,角,,的对边分别为,其中,.(1)求角的值;(2)若,,为边上的任意一点,求的最小值.22.(10分)已知函数.(1)解不等式;(2)若,,,求证:.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、C【解析】作出三棱锥的实物图,然后补成直四棱锥,且底面为矩形,可得知三棱锥的外接球和直四棱锥的外接球为同一个球,然后计算出矩形的外接圆直径,利用公式【详解】可计算出外接球的直径,再利用球体的表面积公式即可得出该三棱锥的外接球的表面积.三棱锥的实物图如下图所示:将其补成直四棱锥,底面,,.可知四边形为矩形,且矩形的外接圆直径,且.所以,三棱锥外接球的直径为,因此,该三棱锥的外接球的表面积为....