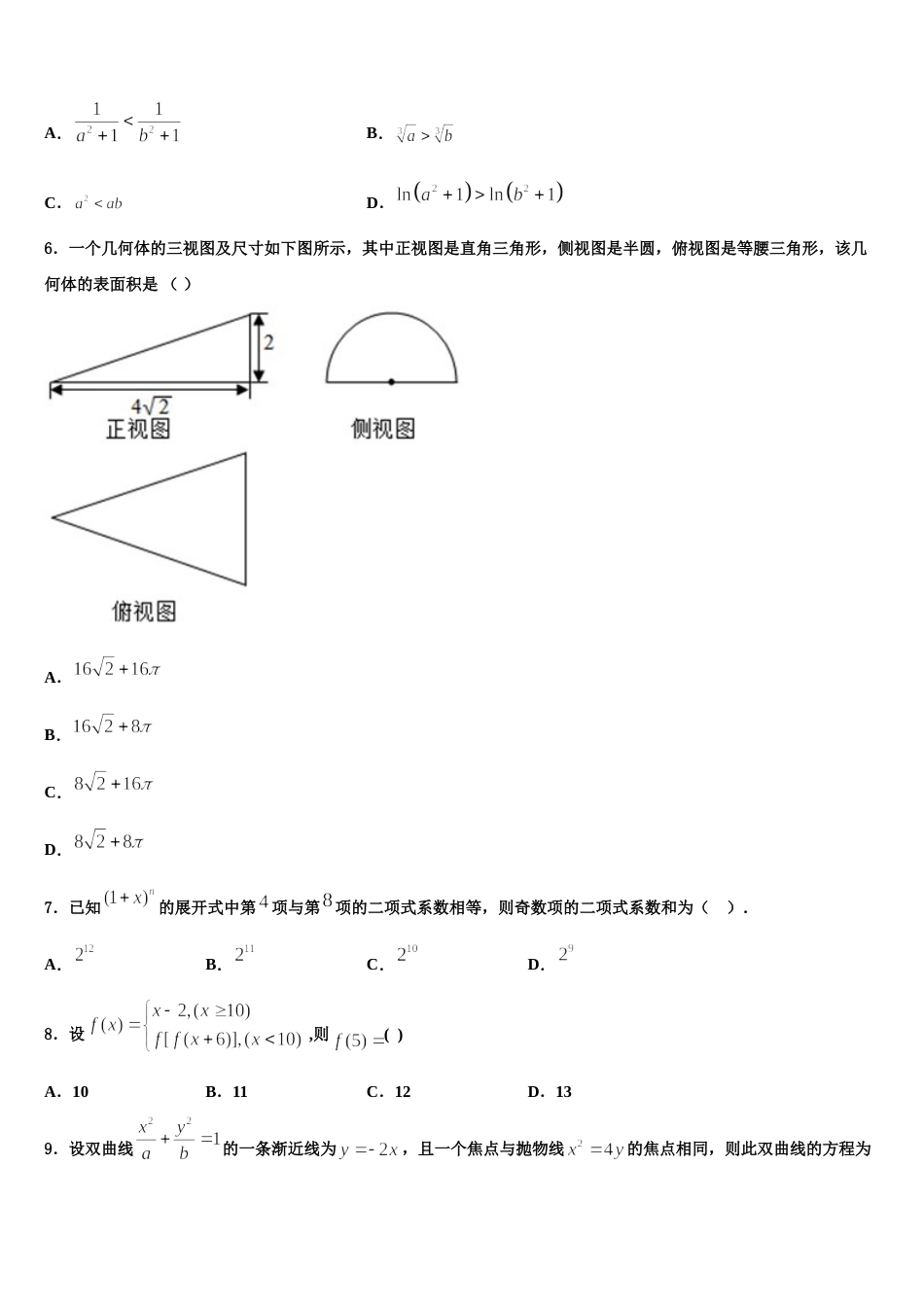
2024 届福建省三明市 A 片区高中联盟校高三第二次模拟考试数学试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用 2B 铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。2.作答选择题时,选出每小题答案后,用 2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试题卷上。3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。不按以上要求作答无效。4.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.设正项等比数列的前 n 项和为,若,,则公比( )A.B.4C.D.22.已知等比数列的前项和为,若,且公比为 2,则与的关系正确的是( )A.B.C.D.3.过双曲线左焦点的直线 交的左支于两点,直线(是坐标原点)交的右支于点,若,且,则的离心率是( )A.B.C.D.4.若 2m>2n>1,则( )A.B.πm﹣n>1C.ln(m﹣n)>0D.5.已知函数,若,则下列不等关系正确的是( )A.B.C.D.6.一个几何体的三视图及尺寸如下图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的表面积是 ( ) A.B.C.D.7.已知的展开式中第项与第项的二项式系数相等,则奇数项的二项式系数和为( ).A.B.C.D.8.设 ,则( )A.10B.11C.12D.139.设双曲线的一条渐近线为,且一个焦点与抛物线的焦点相同,则此双曲线的方程为( )A.B.C.D.10.设命题 p:>1,n2>2n,则p 为( )A.B.C.D.11.已知集合,,若,则( )A.或B.或C. 或D. 或12.已知集合则( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.点是曲线()图象上的一个定点,过点的切线方程为,则实数 k 的值为______.14.某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品,制作过程必须先后经过两次烧制,当第一次烧制合格后方可进入第二次烧制,再次烧制过程相互独立.根据该厂现有的技术水平,经过第一次烧制后,甲、乙、丙三件产品合格的概率依次为 0.5、0.6、0.4,经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为 0.6、0.5、0.75;则第一次烧制后恰有一件产品合格的概率为________;经过前后两次烧制后,合格工艺品的件数为,则随机变量的期望为________.15.双曲线的焦距为__________,渐近线方程为________.16.在长方体中,,,,为的中点,则点到平面的距离是______.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)如图,在四棱锥 P-ABCD 中,底面 ABCD 是边长为 2 的菱形,,为等边三角形,平面平面 ABCD,M,N 分别是线段 PD 和 BC 的中点.(1)求直线 CM 与平面 PAB 所成角的正弦值;(2)求二面角 D-AP-B 的余弦值;(3)试判断直线 MN 与平面 PAB 的位置关系,并给出证明.18.(12 分)如图,在等腰梯形中,AD BC∥,,,,,分别为,,的中点,以为折痕将折起,使点到达点位置(平面).(1)若为直线上任意一点,证明:MH∥平面;(2)若直线与直线所成角为,求二面角的余弦值.19.(12 分)已知是圆:的直径,动圆过,两点,且与直线相切.(1)若直线的方程为,求的方程;(2)在轴上是否存在一个定点,使得以为直径的圆恰好与轴相切?若存在,求出点的坐标;若不存在,请说明理由.20.(12 分)已知函数(1)已知直线 :,:.若直线与关于 对称,又函数在处的切线与垂直,求实数的值;(2)若函数,则当,时,求证:①;②.21.(12 分)已知函数,(1)证明:在区间单调递减;(2)证明:对任意的有.22.(10 分)已知首项为 2 的数列满足.(1)证明:数列是等差数列.(2)令,求数列的前项和.参考答案一、选择题:本...