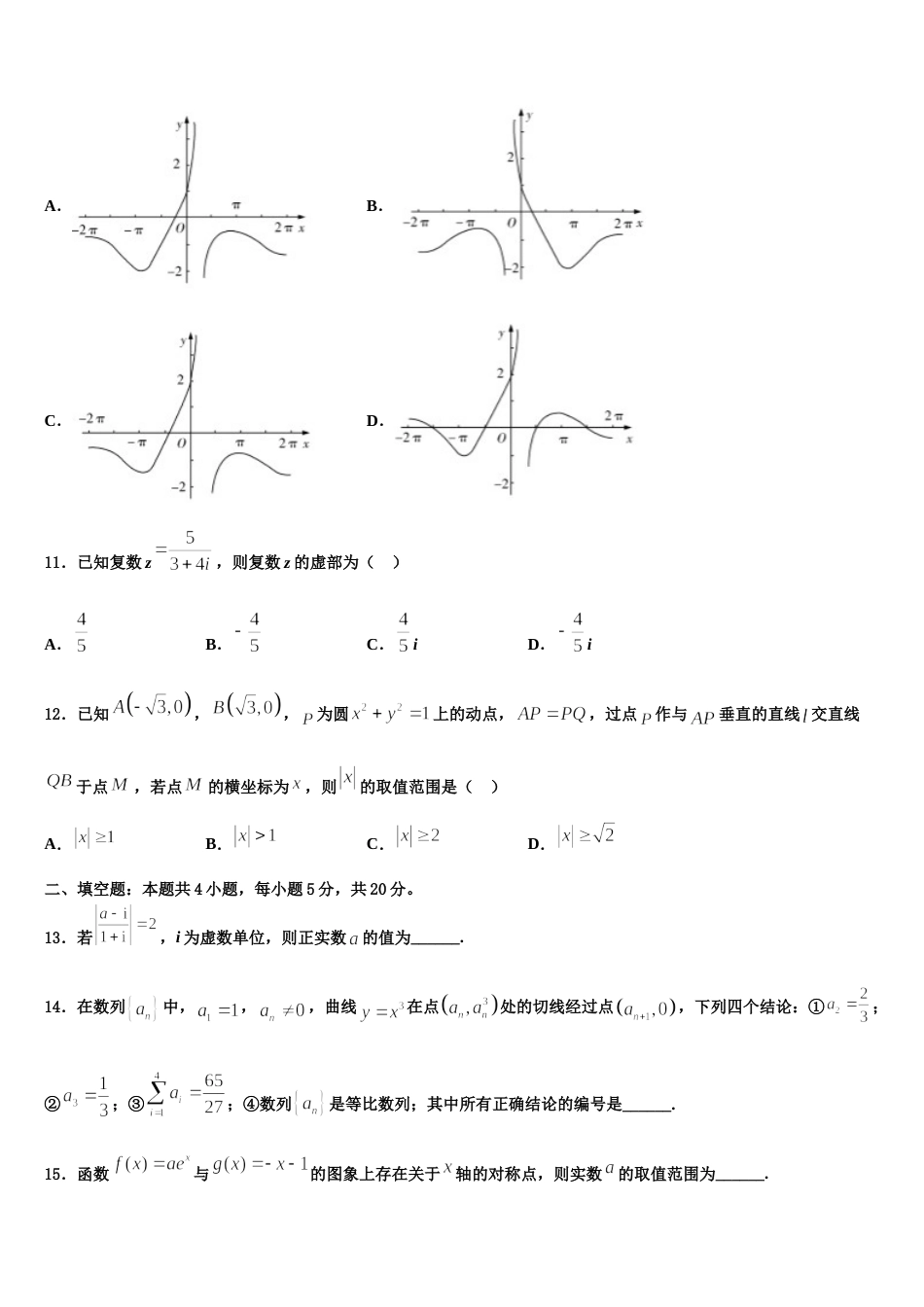
2024 届福建省厦门市思明区夏门一中高三下第一次测试数学试题请考生注意:1.请用 2B 铅笔将选择题答案涂填在答题纸相应位置上,请用 0.5 毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.函数的部分图象大致为( )A.B.C.D.2.设等差数列的前项和为,若,则( )A.23B.25C.28D.293.若复数满足,则( )A.B.C.2D.4.若复数 z 满足,则复数 z 在复平面内对应的点在( )A.第一象限B.第二象限C.第三象限D.第四象限5.如图,网格纸上小正方形的边长为 ,粗实线画出的是某几何体的三视图,则该几何体的体积为( )A.B.C.D.6.如图,在平面四边形 ABCD 中,若点 E 为边 CD 上的动点,则的最小值为 ( )A.B.C.D.7.已知椭圆:的左、右焦点分别为,,过的直线与轴交于点,线段与交于点.若,则的方程为( )A.B.C.D.8.已知函数,,若成立,则的最小值是( )A.B.C.D.9.已知双曲线,为坐标原点,、为其左、右焦点,点在的渐近线上,,且,则该双曲线的渐近线方程为( )A.B.C.D.10.函数在的图象大致为A.B.C.D.11.已知复数 z,则复数 z 的虚部为( )A.B.C.iD.i12.已知,,为圆上的动点,,过点作与垂直的直线 交直线于点,若点的横坐标为,则的取值范围是( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.若,i 为虚数单位,则正实数的值为______.14.在数列中,,,曲线在点处的切线经过点,下列四个结论:①;②;③;④数列是等比数列;其中所有正确结论的编号是______.15.函数与的图象上存在关于轴的对称点,则实数的取值范围为______.16.已知均为非负实数,且,则的取值范围为______.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知,,分别为内角,,的对边,若同时满足下列四个条件中的三个:①;②;③;④.(1)满足有解三角形的序号组合有哪些?(2)在(1)所有组合中任选一组,并求对应的面积.(若所选条件出现多种可能,则按计算的第一种可能计分)18.(12 分)选修 4-5:不等式选讲设函数.(1) 证明:;(2)若不等式的解集非空,求 的取值范围.19.(12 分)求下列函数的导数:(1)(2)20.(12 分)已知函数,.(1)判断函数在区间上的零点的个数;(2)记函数在区间上的两个极值点分别为、,求证:.21.(12 分)已知中,角所对边的长分别为,且(1)求角的大小;(2)求的值.22.(10 分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶 4 元,售价每瓶 6 元,未售出的酸奶降价处理,以每瓶 2 元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于 25,需求量为 500 瓶;如果最高气温位于区间[20,25),需求量为 300 瓶;如果最高气温低于20,需求量为 200 瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:最高气温[10,15)[15,20)[20,25)[25,30)[30,35)[35,40)天数216362574以最高气温位于各区间的频率估计最高气温位于该区间的概率.(1)求六月份这种酸奶一天的需求量不超过 300 瓶的概率;(2)设六月份一天销售这种酸奶的利润为 Y(单位:元),当六月份这种酸奶一天的进货量为 450 瓶时,写出 Y 的所有可能值,并估计 Y 大于零的概率.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、B【解析】图像分析采用排除法,利用奇偶性判断函数为奇函数,再利用特值确定函数的正负情况。【详解】,故奇函数,四个图像均符合。当时,,,排除 C、D当时,,,排除 A。故选 B。【点睛】图像分析采用排除法,一般可供判断的主要有...