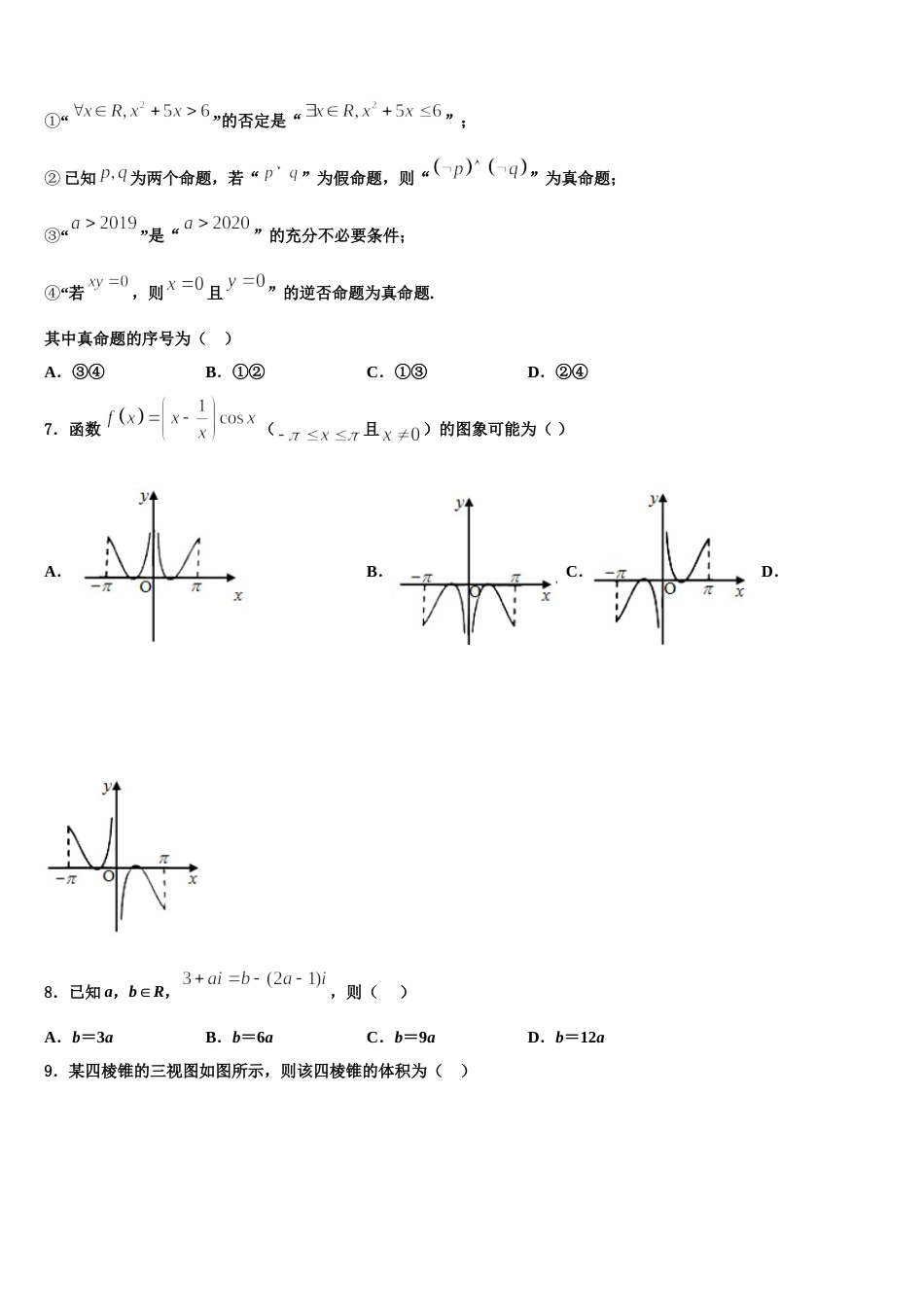
2024 届福建省宁德市重点名校高三下学期第五次调研考试数学试题请考生注意:1.请用 2B 铅笔将选择题答案涂填在答题纸相应位置上,请用 0.5 毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知中,,则( )A.1B.C.D.2.若与互为共轭复数,则( )A.0B.3C.-1D.43.已知集合,若,则实数的取值范围为( )A.B.C.D.4.已知复数在复平面内对应的点的坐标为,则下列结论正确的是( )A.B.复数的共轭复数是C.D.5.过双曲线的右焦点 F 作双曲线 C 的一条弦 AB,且,若以 AB 为直径的圆经过双曲线 C 的左顶点,则双曲线 C 的离心率为( )A.B.C.2D.6.已知下列命题:①“”的否定是“”;② 已知为两个命题,若“”为假命题,则“”为真命题;③“”是“”的充分不必要条件;“④ 若,则且”的逆否命题为真命题.其中真命题的序号为( )A.③④B.①②C.①③D.②④7.函数(且)的图象可能为( )A.B.C.D.8.已知 a,b∈R,,则( )A.b=3aB.b=6aC.b=9aD.b=12a9.某四棱锥的三视图如图所示,则该四棱锥的体积为( )A.B.C.D.10.已知双曲线,为坐标原点,、为其左、右焦点,点在的渐近线上,,且,则该双曲线的渐近线方程为( )A.B.C.D.11.方程在区间内的所有解之和等于( )A.4B.6C.8D.1012.对于正在培育的一颗种子,它可能 1 天后发芽,也可能 2 天后发芽,….下表是 20 颗不同种子发芽前所需培育的天数统计表,则这组种子发芽所需培育的天数的中位数是( )发芽所需天数1234567种子数43352210A.2B.3C.3.5D.4二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.数学家狄里克雷对数论,数学分析和数学物理有突出贡献,是解析数论的创始人之一.函数,称为狄里克雷函数.则关于有以下结论:①的值域为;②;③;④其中正确的结论是_______(写出所有正确的结论的序号)14.设全集,,,则______.15.如图在三棱柱中,,,,点为线段上一动点,则的最小值为________.16.已知随机变量,且,则______三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)在中,角的对边分别为.已知,且.(1)求的值;(2)若的面积是,求的周长.18.(12 分)已知数列满足,.(1)求数列的通项公式;(2)若,求数列的前项和.19.(12 分)已知椭圆的左,右焦点分别为,直线与椭圆相交于两点;当直线 经过椭圆的下顶点和右焦点时,的周长为,且 与椭圆的另一个交点的横坐标为(1)求椭圆的方程;(2)点为内一点,为坐标原点,满足,若点恰好在圆上,求实数的取值范围.20.(12 分)在直角坐标系中,已知曲线的参数方程为(为参数),以原点为极点,轴的非负半轴为极轴建立极坐标系,射线的极坐标方程为,射线的极坐标方程为.(Ⅰ)写出曲线的极坐标方程,并指出是何种曲线;(Ⅱ)若射线与曲线交于两点,射线与曲线交于两点,求面积的取值范围.21.(12 分)已知数列是公比为正数的等比数列,其前项和为,满足,且成等差数列.(1)求的通项公式;(2)若数列满足,求的值.22.(10 分)一年之计在于春,一日之计在于晨,春天是播种的季节,是希望的开端.某种植户对一块地的个坑进行播种,每个坑播 3 粒种子,每粒种子发芽的概率均为,且每粒种子是否发芽相互独立.对每一个坑而言,如果至少有两粒种子发芽,则不需要进行补播种,否则要补播种.(1)当取何值时,有 3 个坑要补播种的概率最大?最大概率为多少?(2)当时,用表示要补播种的坑的个数,求的分布列与数学期望.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、C【解析】以为基底,将用基底表示,根据向量数量积的运算律,即可求解.【详解】,,.故选:C.【点睛】本题考查向量的线性运...