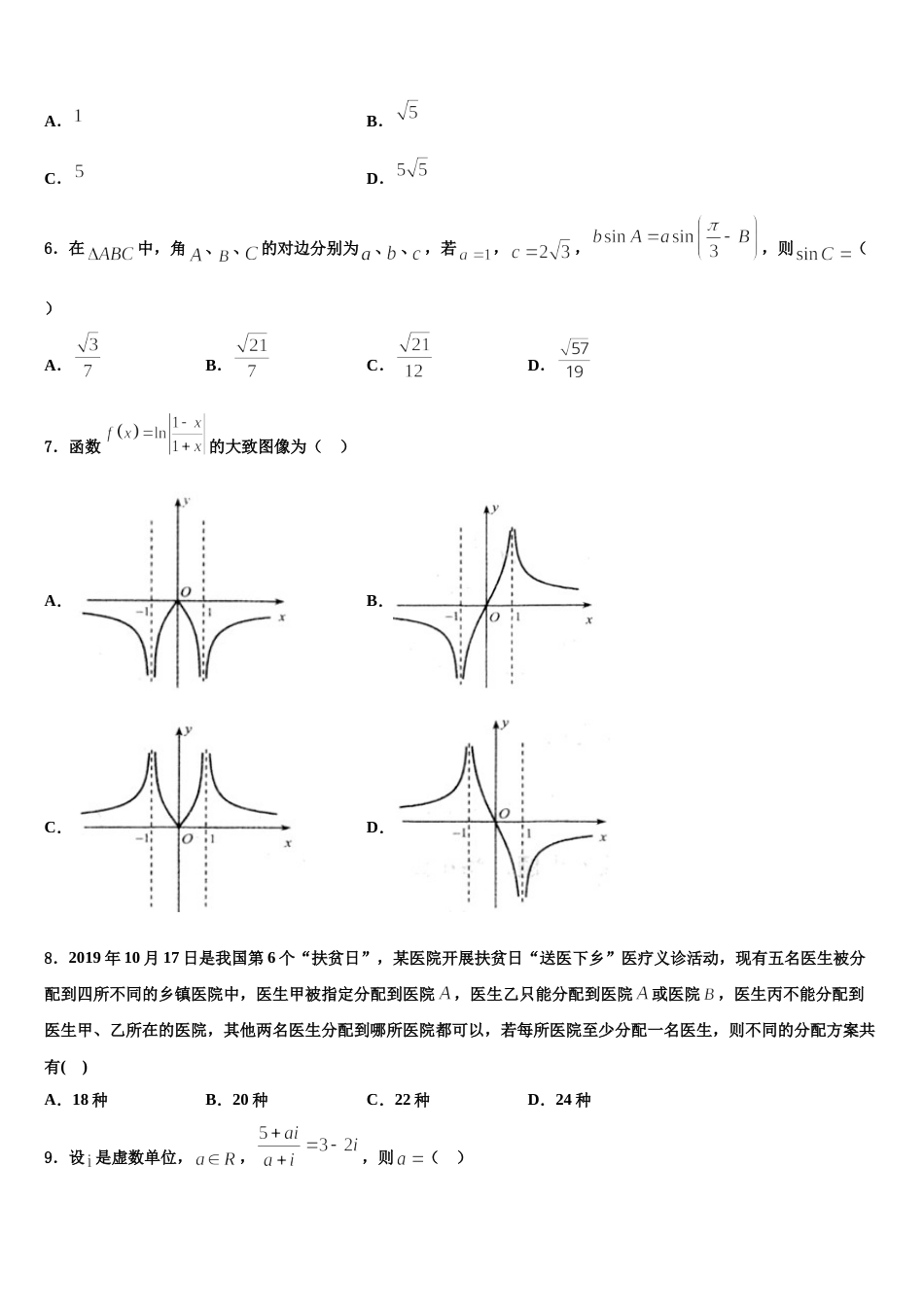
2024 届福建省永春一中等四校中学高三下学期一模考试数学试题请考生注意:1.请用 2B 铅笔将选择题答案涂填在答题纸相应位置上,请用 0.5 毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.设函数,则,的大致图象大致是的( )A.B.C.D.2.已知双曲线,为坐标原点,、为其左、右焦点,点在的渐近线上,,且,则该双曲线的渐近线方程为( )A.B.C.D.3.已知数列对任意的有成立,若,则等于( )A.B.C.D.4.已知正项等比数列的前项和为,则的最小值为( )A.B.C.D.5.已知 为虚数单位,若复数,,则A.B.C.D.6.在中,角、 、 的对边分别为、 、 ,若,,,则( )A.B.C.D.7.函数的大致图像为( )A.B.C.D.8.2019 年 10 月 17 日是我国第 6 个“扶贫日”,某医院开展扶贫日“送医下乡”医疗义诊活动,现有五名医生被分配到四所不同的乡镇医院中,医生甲被指定分配到医院,医生乙只能分配到医院或医院,医生丙不能分配到医生甲、乙所在的医院,其他两名医生分配到哪所医院都可以,若每所医院至少分配一名医生,则不同的分配方案共有( )A.18 种B.20 种C.22 种D.24 种9.设 是虚数单位,,,则( )A.B.C.1D.210.已知椭圆内有一条以点为中点的弦,则直线的方程为( )A.B.C.D.11.已知函数,则( )A.B.C.D.12.已知向量,满足||=1,||=2,且与的夹角为 120°,则=( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知复数( 为虚数单位)为纯虚数,则实数的值为_____.14.割圆术是估算圆周率的科学方法,由三国时期数学家刘徽创立,他用圆内接正多边形面积无限逼近圆面积,从而得出圆周率.现在半径为 1 的圆内任取一点,则该点取自其内接正十二边形内部的概率为________.15.已知实数,满足约束条件,则的最大值是__________.16.已知四棱锥,底面四边形为正方形,,四棱锥的体积为,在该四棱锥内放置一球,则球体积的最大值为_________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)如图,三棱柱中,与均为等腰直角三角形,,侧面是菱形.(1)证明:平面平面;(2)求二面角的余弦值.18.(12 分)在中,角所对的边分别为,,的面积.(1)求角 C;(2)求周长的取值范围.19.(12 分)已知数列满足且(1)求数列的通项公式;(2)求数列的前项和.20.(12 分)每年 3 月 20 日是国际幸福日,某电视台随机调查某一社区人们的幸福度.现从该社区群中随机抽取 18 名,用“10 分制”记录了他们的幸福度指数,结果见如图所示茎叶图,其中以小数点前的一位数字为茎,小数点后的一位数字为叶.若幸福度不低于 8.5 分,则称该人的幸福度为“很幸福”.( )Ⅰ 求从这 18 人中随机选取 3 人,至少有 1 人是“很幸福”的概率;()Ⅱ 以这 18 人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选 3 人,记表示抽到“很幸福”的人数,求的分布列及.21.(12 分)在中,、、分别是角、、的对边,且.(1)求角的值;(2)若,且为锐角三角形,求的取值范围.22.(10 分)如图,在四棱锥 P—ABCD 中,四边形 ABCD 为平行四边形,BD⊥DC,△PCD 为正三角形,平面PCD⊥平面 ABCD,E 为 PC 的中点. (1)证明:AP∥平面 EBD;(2)证明:BE⊥PC.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、B【解析】采用排除法:通过判断函数的奇偶性排除选项 A;通过判断特殊点的函数值符号排除选项 D 和选项 C即可求解.【详解】对于选项 A:由题意知,函数的定义域为,其关于原点对称,因为,所以函数为奇函数,其图象关于原点对称,故选 A 排除;对于选项 D:因为,故选项 D 排除;对...