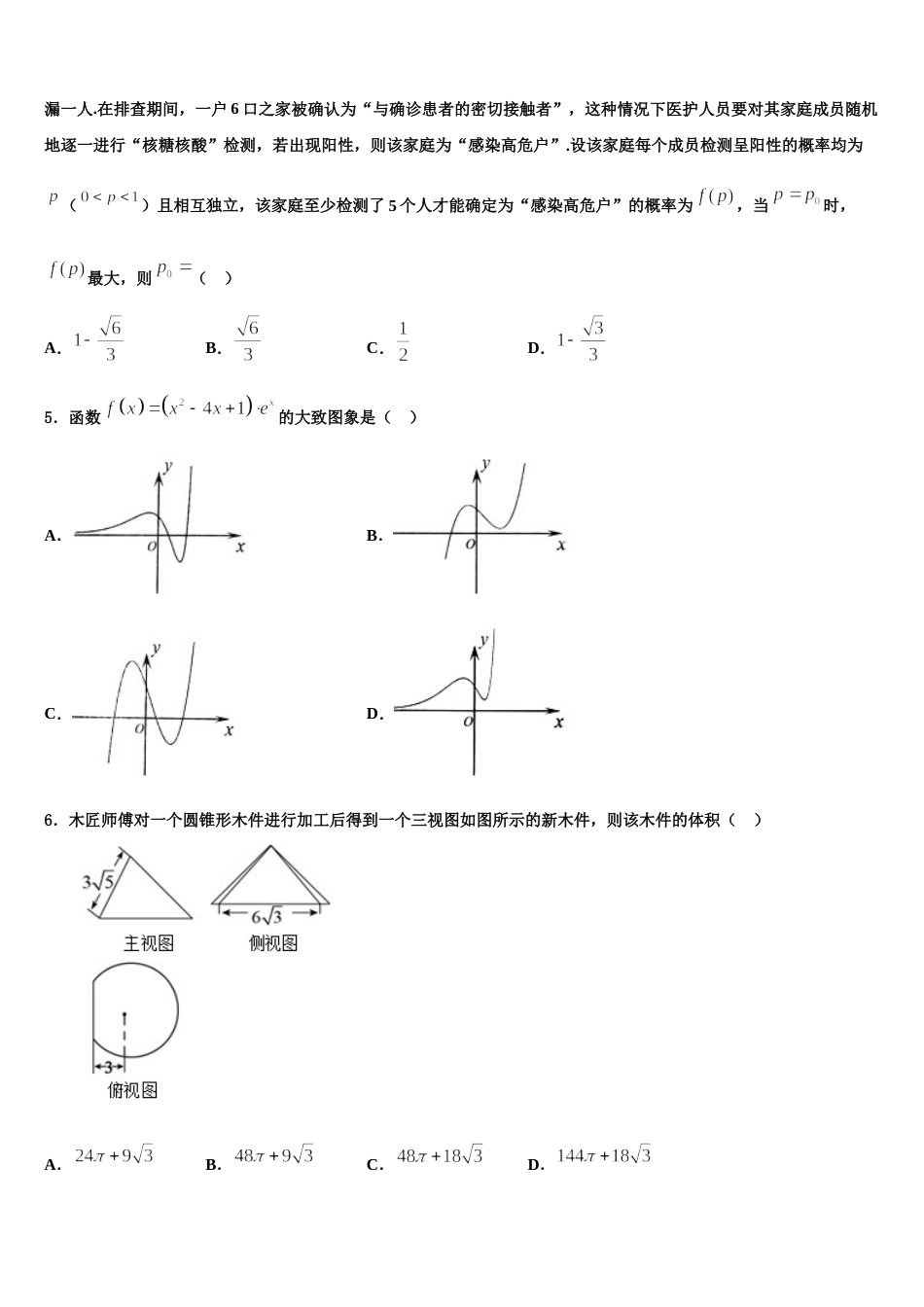
2024 届福建省福州市第十中学高考数学押题试卷注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。2.答题时请按要求用笔。3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知平面向量,满足且,若对每一个确定的向量,记的最小值为,则当变化时,的最大值为( )A.B.C.D.12.已知集合 A={y|y},B={x|y=lg(x2﹣ x2)},则∁R(A∩B)=( )A.[0,)B.(﹣∞,0)∪[,+∞)C.(0,)D.(﹣∞,0]∪[,+∞)3.已知定义在上的奇函数满足:(其中),且在区间上是减函数,令,,,则,,的大小关系(用不等号连接)为( )A.B.C.D.4.2019 年末,武汉出现新型冠状病毒肺炎()疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,所以目前没有特异治疗方法,防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从 2 月 7 日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和与确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,一户 6 口之家被确认为“与确诊患者的密切接触者”,这种情况下医护人员要对其家庭成员随机地逐一进行“核糖核酸”检测,若出现阳性,则该家庭为“感染高危户”.设该家庭每个成员检测呈阳性的概率均为()且相互独立,该家庭至少检测了 5 个人才能确定为“感染高危户”的概率为,当时,最大,则( )A.B.C.D.5.函数的大致图象是( )A.B.C.D.6.木匠师傅对一个圆锥形木件进行加工后得到一个三视图如图所示的新木件,则该木件的体积( ) A.B.C.D.7.过直线上一点作圆的两条切线,,,为切点,当直线,关于直线对称时,( )A.B.C.D.8.将函数的图象先向右平移个单位长度,在把所得函数图象的横坐标变为原来的倍,纵坐标不变,得到函数的图象,若函数在上没有零点,则的取值范围是( )A.B.C.D.9.在棱长均相等的正三棱柱中,为的中点,在上,且,则下述结论:①;②;③平面平面:④异面直线与所成角为其中正确命题的个数为( )A.1B.2C.3D.410.已知是定义是上的奇函数,满足,当时, ,则函数在区间上的零点个数是( )A.3B.5C.7D.911.阿波罗尼斯(约公元前 262~190 年)证明过这样的命题:平面内到两定点距离之比为常数的点的轨迹是圆.后人将这个圆称为阿氏圆.若平面内两定点,间的距离为 2,动点与,的距离之比为,当,,不共线时,的面积的最大值是( )A.B.C.D.12.已知,,,若,则正数可以为( )A.4B.23C.8D.17二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.过点,且圆心在直线上的圆的半径为__________.14.设直线 过双曲线的一个焦点,且与的一条对称轴垂直, 与交于两点,为的实轴长的 2 倍,则双曲线的离心率为 .15.若 x,y 均为正数,且,则的最小值为________.16.在中,角,,所对的边分别边,且,设角的角平分线交于点,则的值最小时,___.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)如图在四边形中,,,为中点,.(1)求;(2)若,求面积的最大值.18.(12 分)选修 4-5:不等式选讲已知函数 f(x)=log2(|x+1|+|x2|﹣ ﹣m).(1)当 m=7 时,求函数 f(x)的定义域;(2)若关于 x 的不等式 f(x)≥2 的解集是 R,求 m 的取值范围.19.(12 分)如图 1,四边形为直角梯形,,,,,,为线段上一点,满足,为的中点,现将梯形沿折叠(如图 2),使平面平面.(1)求证:平面平面;(2)能否在线段上找到一点(端点除外)使得直线...