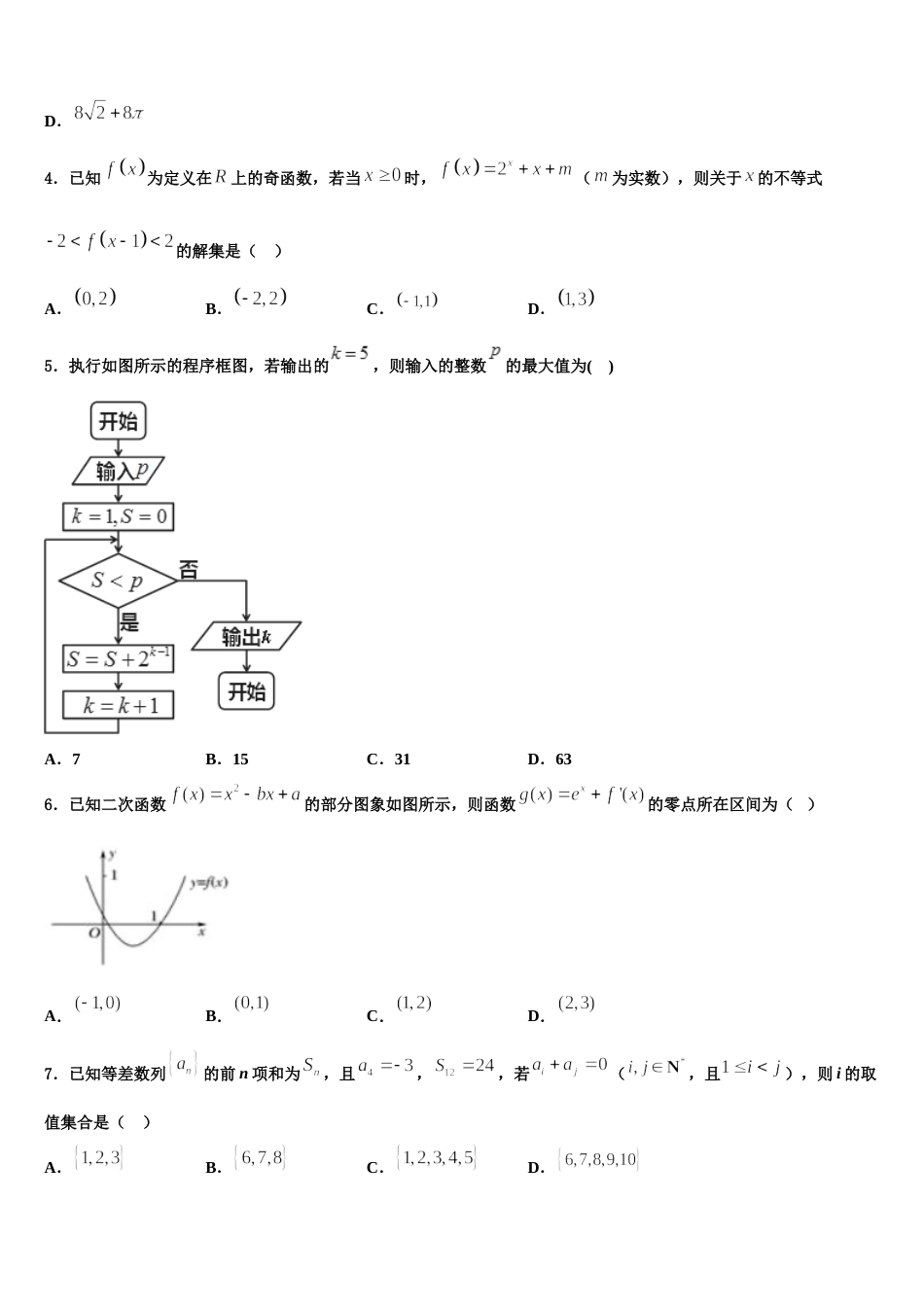
2024 届福建省福州第一中学高三下学期联合考试数学试题考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.a 为正实数,i 为虚数单位,,则 a=( )A.2B.C.D.12.在中,角、、所对的边分别为、、,若,则( )A.B.C.D.3.一个几何体的三视图及尺寸如下图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的表面积是 ( ) A.B.C.D.4.已知为定义在上的奇函数,若当时,(为实数),则关于的不等式的解集是( )A.B.C.D.5.执行如图所示的程序框图,若输出的,则输入的整数的最大值为( )A.7B.15C.31D.636.已知二次函数的部分图象如图所示,则函数的零点所在区间为( )A.B.C.D.7.已知等差数列的前 n 项和为,且,,若(,且),则 i 的取值集合是( )A.B.C.D.8.下图是来自古希腊数学家希波克拉底所研究的几何图形,此图由三个半圆构成,三个半圆的直径分别为直角三角形的斜边、直角边,已知以直角边为直径的半圆的面积之比为,记,则( )A.B.C.1D.9.若函数的定义域为 M={x|-2≤x≤2},值域为 N={y|0≤y≤2},则函数的图像可能是( )A.B.C.D.10.在中,内角 A,B,C 所对的边分别为 a,b,c,D 是 AB 的中点,若,且,则面积的最大值是( )A.B.C.D.11.设,,是非零向量.若,则( )A.B.C.D.12.执行下面的程序框图,若输出的的值为 63,则判断框中可以填入的关于 的判断条件是( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.如图,在正四棱柱中,P 是侧棱上一点,且.设三棱锥的体积为,正四棱柱的体积为 V,则的值为________.14.若方程有两个不等实根,则实数的取值范围是_____________.15.在边长为的菱形中,点在菱形所在的平面内.若,则_____.16.设是等比数列的前项的和,成等差数列,则的值为_____.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知各项均为正数的数列的前项和为,且,(,且)(1)求数列的通项公式;(2)证明:当时,18.(12 分)某调查机构对某校学生做了一个是否同意生“二孩”抽样调查,该调查机构从该校随机抽查了 100 名不同性别的学生,调查统计他们是同意父母生“二孩”还是反对父母生“二孩”,现已得知 100 人中同意父母生“二孩”占 60%,统计情况如下表:同意不同意合计男生a5女生40d合计100(1)求 a,d 的值,根据以上数据,能否有 97.5%的把握认为是否同意父母生“二孩”与性别有关?请说明理由;(2)将上述调查所得的频率视为概率,现在从所有学生中,采用随机抽样的方法抽取 4 位学生进行长期跟踪调查,记被抽取的 4 位学生中持“同意”态度的人数为 X,求 X 的分布列及数学期望.附:0.150.1000.0500.0250.0102.0722.7063.8415.0246.63519.(12 分)如图,四边形是边长为 3 的菱形,平面.(1)求证:平面;(2)若与平面所成角为,求二面角的正弦值.20.(12 分)已知函数.(1)当时,求函数在处的切线方程;(2)若函数没有零点,求实数的取值范围.21.(12 分)为了解本学期学生参加公益劳动的情况,某校从初高中学生中抽取 100 名学生,收集了他们参加公益劳动时间(单位:小时)的数据,绘制图表的一部分如表.(1)从男生中随机抽取一人,抽到的男生参加公益劳动时间在的概率:(2)从参加公益劳动时间的学生中抽取 3 人进行面谈,记为抽到高中的人数,求的分布列;(3)当时,高中生和初中生相比,那学段学生平均参加公益劳动时间较长.(直接写出结果)22.(10 分)已知,,分别为内角,,的对边,且.(1)证明:;(2)若的面积,,求角...