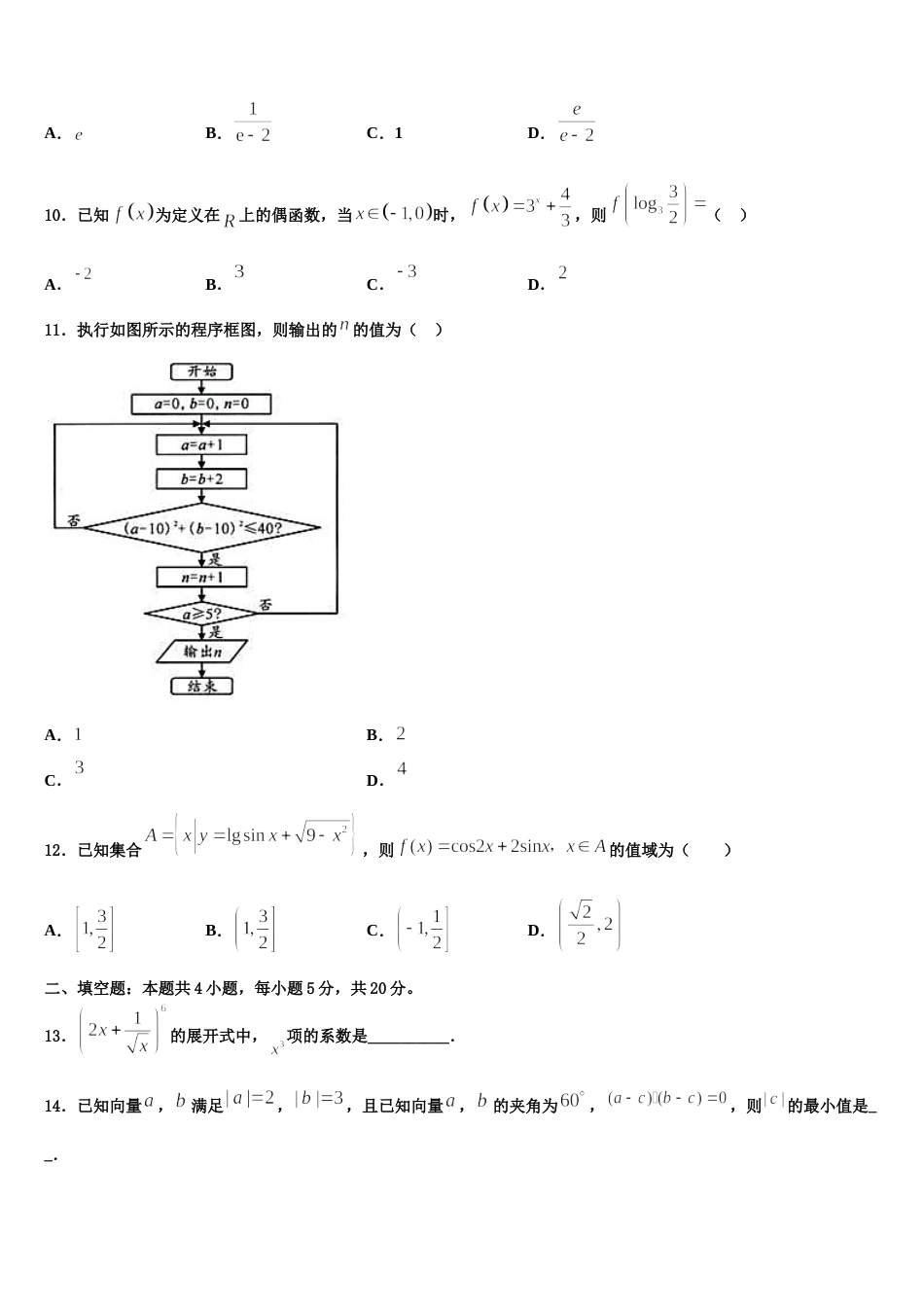
2024 届福建省重点中学高考冲刺模拟数学试题注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用 2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.记的最大值和最小值分别为和.若平面向量、、 ,满足,则( )A.B.C.D.2.已知命题,那么为( )A.B.C.D.3.设函数的导函数,且满足,若在中,,则( )A.B.C.D.4.已知的内角、、的对边分别为、 、 ,且,,为边上的中线,若,则的面积为( )A.B.C.D.5.如图所示,网格纸上小正方形的边长为 ,粗线画出的是某多面体的三视图,则该几何体的各个面中最大面的面积为( )A.B.C.D.6.设是等差数列,且公差不为零,其前项和为.则“,”是“为递增数列”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件7.已知 是虚数单位,则( )A.B.C.D.8.若将函数的图象上各点横坐标缩短到原来的(纵坐标不变)得到函数的图象,则下列说法正确的是( )A.函数在上单调递增B.函数的周期是C.函数的图象关于点对称D.函数在上最大值是 19.已知函数,若所有点,所构成的平面区域面积为,则( )A.B.C.1D.10.已知为定义在上的偶函数,当时,,则( )A.B.C.D.11.执行如图所示的程序框图,则输出的的值为( ) A.B.C.D.12.已知集合,则的值域为( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.的展开式中,项的系数是__________.14.已知向量,满足,,且已知向量,的夹角为,,则的最小值是__.15.连续掷两次骰子,分别得到的点数作为点的坐标,则点落在圆内的概率为______________.16.若,则________,________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知抛物线 E:y2=2px(p>0),焦点 F 到准线的距离为 3,抛物线 E 上的两个动点 A(x1,y1)和B(x2,y2),其中 x1≠x2且 x1+x2=1.线段 AB 的垂直平分线与 x 轴交于点 C.(1)求抛物线 E 的方程;(2)求△ABC 面积的最大值.18.(12 分)已知为椭圆的左、右焦点,离心率为,点在椭圆上.(1)求椭圆的方程;(2)过的直线分别交椭圆于和,且,问是否存在常数,使得成等差数列?若存在,求出的值;若不存在,请说明理由.19.(12 分)如图,在中,,,点在线段上.(1)若,求的长;(2)若,,求的面积.20.(12 分)如图,在直角中,,,,点在线段上.(1)若,求的长;(2)点是线段上一点,,且,求的值.21.(12 分)已知函数(1)若函数在处取得极值 1,证明:(2)若恒成立,求实数的取值范围.22.(10 分)如图,已知四棱锥,底面为边长为 2 的菱形,平面,,是的中点,.(Ⅰ) 证明:;(Ⅱ) 若为上的动点,求与平面所成最大角的正切值.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、A【解析】设为、的夹角,根据题意求得,然后建立平面直角坐标系,设,,,根据平面向量数量积的坐标运算得出点的轨迹方程,将和转化为圆上的点到定点距离,利用数形结合思想可得出结果.【详解】由已知可得,则,,,建立平面直角坐标系,设,,,由,可得,即,化简得点的轨迹方程为,则,则转化为圆上的点与点的距离,,,,转化为圆上的点与点的距离,,.故选:A.【点睛】本题考查和向量与差向量模最值的求解,将向量坐标化,将问题转化为圆上的点到定点距离的最值问题是解答的关键,考查化归与转化思想与数形结合思想的应用,属于中等题.2、B【解析】利用特称命题的否定分析解答得解.【详解】已知命题,,那么是.故选:.【点睛】本题主要考查特称命题的否定,意在考查学生对该知识的理解掌握水平,属于基础题.3、D【解析】根据的结构...