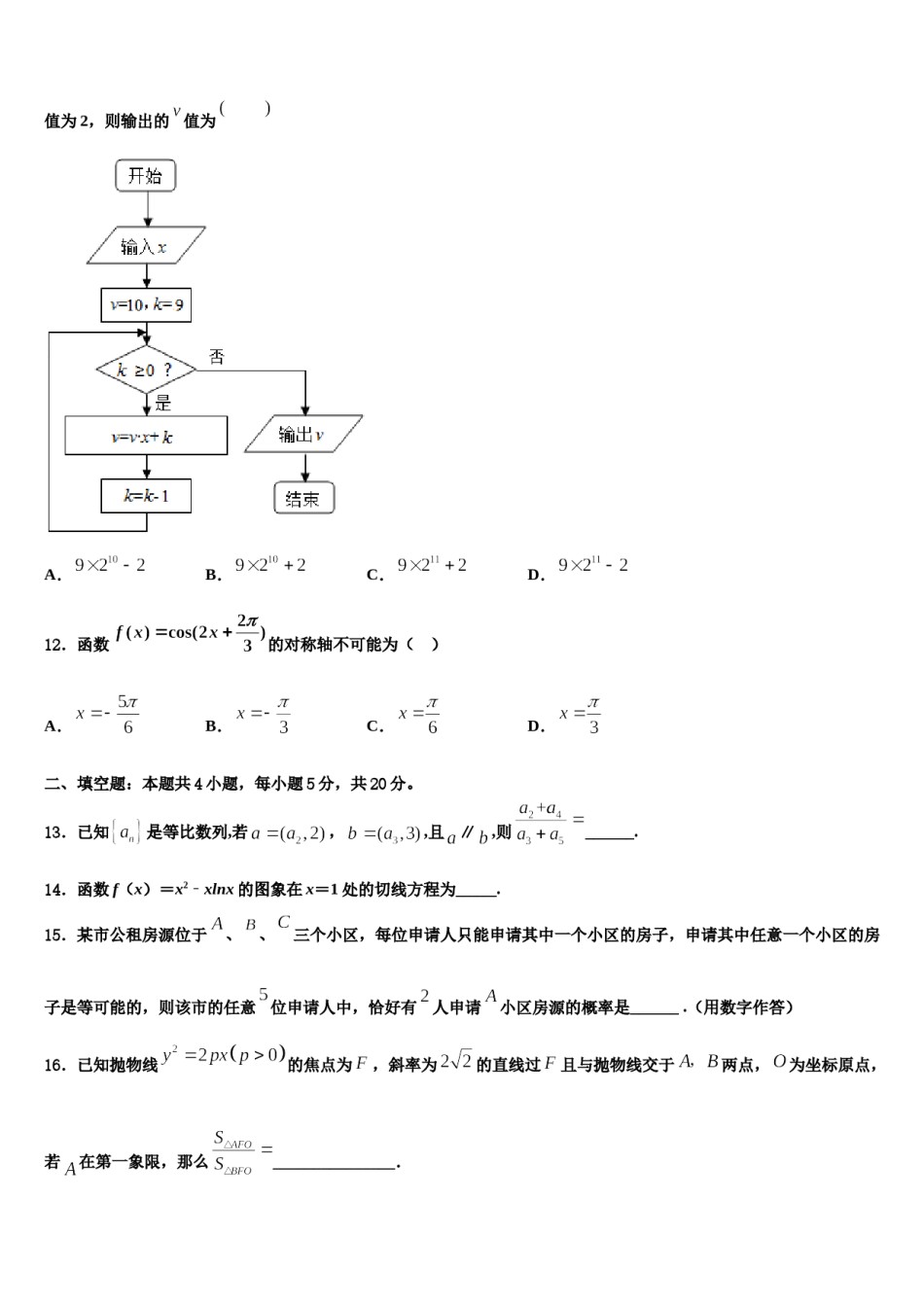
2024届福建省长汀一中等六校高考数学四模试卷注意事项铅笔作答;第二部分必须用黑1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.点是单位圆上不同的三点,线段与线段交于圆内一点M,若,则的最小值为()A.B.C.D.2.已知集合A={xy=lg(4﹣x2)},B={yy=3x,x>0}时,A∩B=()A.{xx>﹣2}B.{x1<x<2}C.{x1≤x≤2}D.∅3.若集合M={1,3},N={1,3,5},则满足M∪X=N的集合X的个数为()A.1B.2C.3D.44.函数的图象与轴交点的横坐标构成一个公差为的等差数列,要得到函数的图象,只需将的图象()A.向左平移个单位B.向右平移个单位C.向左平移个单位D.向右平移个单位5.设是虚数单位,,,则()A.B.C.1D.26.双曲线的渐近线方程为()A.B.C.D.7.已知(),i为虚数单位,则()A.B.3C.1D.58.已知命题:,,则为()A.,B.,C.,D.,9.观察下列各式:,,,,,,,,根据以上规律,则()A.B.C.D.10.用数学归纳法证明,则当时,左端应在的基础上加上()A.B.C.D.11.秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入的值为2,则输出的值为A.B.C.D.12.函数的对称轴不可能为()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.已知是等比数列,若,,且∥,则______.14.函数f(x)=x2﹣xlnx的图象在x=1处的切线方程为_____.15.某市公租房源位于、、三个小区,每位申请人只能申请其中一个小区的房子,申请其中任意一个小区的房子是等可能的,则该市的任意位申请人中,恰好有人申请小区房源的概率是______.(用数字作答)16.已知抛物线的焦点为,斜率为的直线过且与抛物线交于两点,为坐标原点,若在第一象限,那么_______________.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,PA⊥底面ABCD,∠BAD=60°,AB=PA=4,E是PA的中点,AC,BD交于点O.(1)求证:OE∥平面PBC;,若的解集为.(2)求三棱锥E﹣PBD的体积.,求证:18.(12分)已知函数.(1)求的值;(2)若正实数,,满足19.(12分)已知函数.(1)当时,求不等式的解集;(2)若对任意成立,求实数的取值范围.20.(12分)在某外国语学校举行的(高中生数学建模大赛)中,参与大赛的女生与男生人数之比为,且成绩分布在,分数在以上(含)的同学获奖.按女生、男生用分层抽样的方法抽取人的成绩作为样本,得到成绩的频率分布直方图如图所示.(Ⅰ)求的值,并计算所抽取样本的平均值(同一组中的数据用该组区间的中点值作代表);(Ⅱ)填写下面的列联表,并判断在犯错误的概率不超过的前提下能否认为“获奖与女生、男生有关”.获奖女生男生总计不获奖总计附表及公式:其中,.21.(12分)在中,,,.求边上的高.①,②,③,这三个条件中任选一个,补充在上面问题中并作答.22.(10分)已知,,设函数,.(1)若,求不等式的解集;(2)若函数的最小值为1,证明:.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、D【解析】由题意得,再利用基本不等式即可求解.【详解】将平方得,(当且仅当时等号成立),,的最小值为,故选:D.【点睛】本题主要考查平面向量数量积的应用,考查基本不等式的应用,属于中档题.2、B【解析】试题分析:由集合A中的函数,得到,解得:,∴集合,则,由集合B中的函数,得到,∴集合,故选B.考点:交集及其运算.共4个,选D.3、D【解析】可以是4、A【解析】依题意有的周期为.而5、C,可得,故应左移.【解析】,,通过等号左右实部和虚部分别相等即可求出由的值.【详...