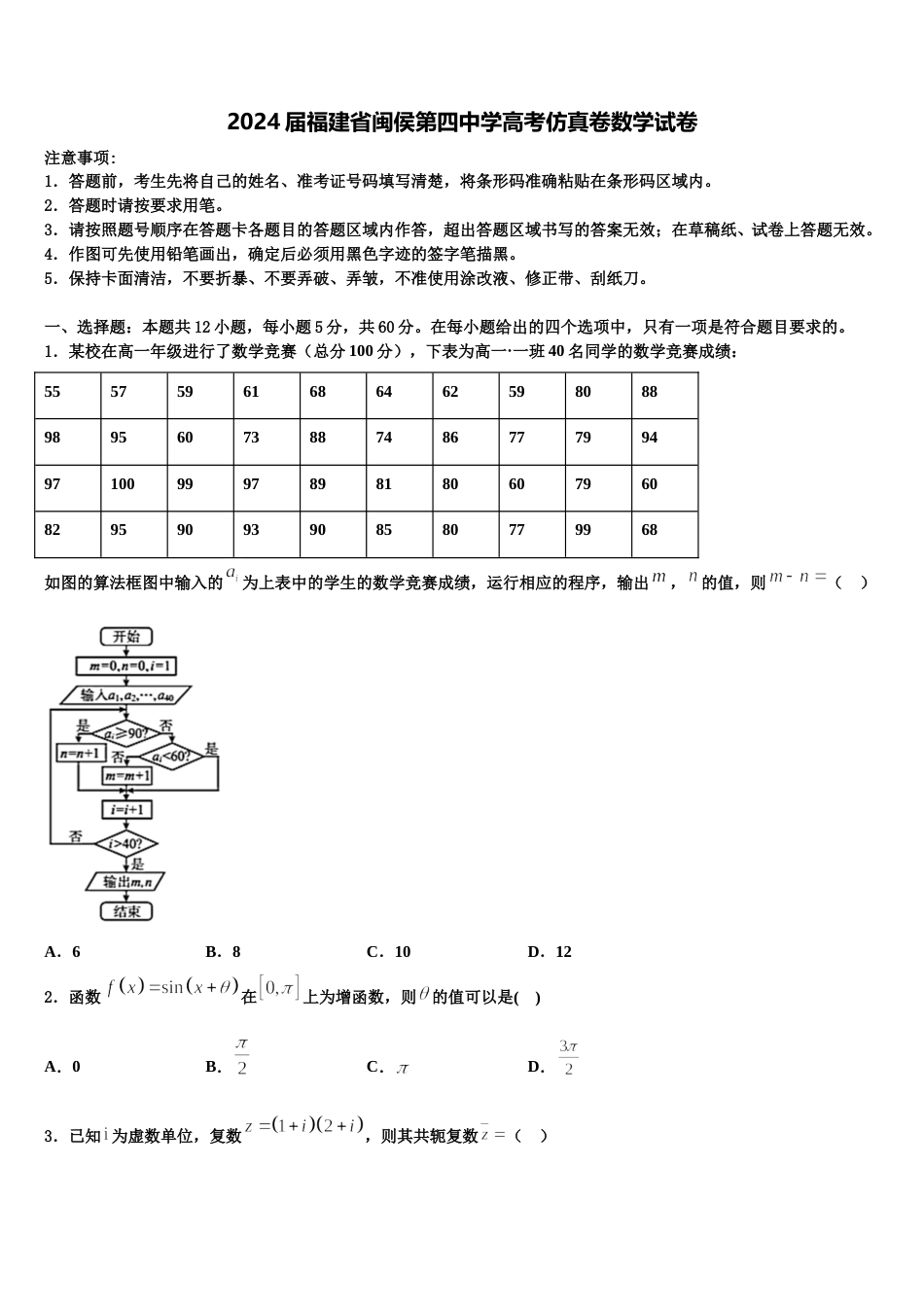
2024 届福建省闽侯第四中学高考仿真卷数学试卷注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。2.答题时请按要求用笔。3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.某校在高一年级进行了数学竞赛(总分 100 分),下表为高一·一班 40 名同学的数学竞赛成绩:555759616864625980889895607388748677799497100999789818060796082959093908580779968如图的算法框图中输入的为上表中的学生的数学竞赛成绩,运行相应的程序,输出,的值,则( )A.6B.8C.10D.122.函数在上为增函数,则的值可以是( )A.0B.C.D.3.已知 为虚数单位,复数,则其共轭复数( )A.B.C.D.4.某三棱锥的三视图如图所示,网格纸上小正方形的边长为 ,则该三棱锥外接球的表面积为( )A.B.C.D.5.命题:存在实数,对任意实数,使得恒成立;:,为奇函数,则下列命题是真命题的是( )A.B.C.D.6.已知,且,则的值为( )A.B.C.D.7.在中,已知,,,为线段上的一点,且,则的最小值为( )A.B.C.D.8.如图,在棱长为 4 的正方体中,E,F,G 分别为棱 AB,BC,的中点,M 为棱 AD 的中点,设 P,Q 为底面 ABCD 内的两个动点,满足平面 EFG,,则的最小值为( )A.B.C.D.9.设双曲线(a>0,b>0)的一个焦点为 F(c,0)(c>0),且离心率等于,若该双曲线的一条渐近线被圆 x2+y22﹣ cx=0 截得的弦长为 2,则该双曲线的标准方程为( )A.B.C.D.10.已知是椭圆和双曲线的公共焦点,是它们的-一个公共点,且,设椭圆和双曲线的离心率分别为,则的关系为( )A.B.C.D.11.设函数是奇函数的导函数,当时,,则使得成立的的取值范围是( )A.B.C.D.12.已知(i 为虚数单位,),则 ab 等于( )A.2B.-2C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知双曲线的一条渐近线为,且经过抛物线的焦点,则双曲线的标准方程为______.14.某中学数学竞赛培训班共有 10 人,分为甲、乙两个小组,在一次阶段测试中两个小组成绩的茎叶图如图所示,若甲组 5 名同学成绩的平均数为 81,乙组 5 名同学成绩的中位数为 73,则 x- y 的值为________.15.已知实数满足( 为虚数单位),则的值为_______.16.某校高三年级共有名学生参加了数学测验(满分分),已知这名学生的数学成绩均不低于分,将这名学生的数学成绩分组如下:,,,,,,得到的频率分布直方图如图所示,则下列说法中正确的是________(填序号).①;② 这名学生中数学成绩在分以下的人数为;③ 这名学生数学成绩的中位数约为;④ 这名学生数学成绩的平均数为.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)若数列前 n 项和为,且满足(t 为常数,且)(1)求数列的通项公式:(2)设,且数列为等比数列,令,.求证:.18.(12 分)如图,空间几何体中,是边长为 2 的等边三角形,,,,平面平面,且平面平面,为中点.(1)证明:平面;(2)求二面角平面角的余弦值.19.(12 分)已知函数.(1)若关于的不等式的整数解有且仅有一个值,当时,求不等式的解集;(2)已知,若,使得成立,求实数的取值范围.20.(12 分) [2018·石家庄一检]已知函数.(1)若,求函数的图像在点处的切线方程;(2)若函数有两个极值点,,且,求证:.21.(12 分)求函数的最大值.22.(10 分)已知函数,其导函数为,(1)若,求不等式的解集;(2)证明:对任意的,恒有.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、D【解析】根据程...