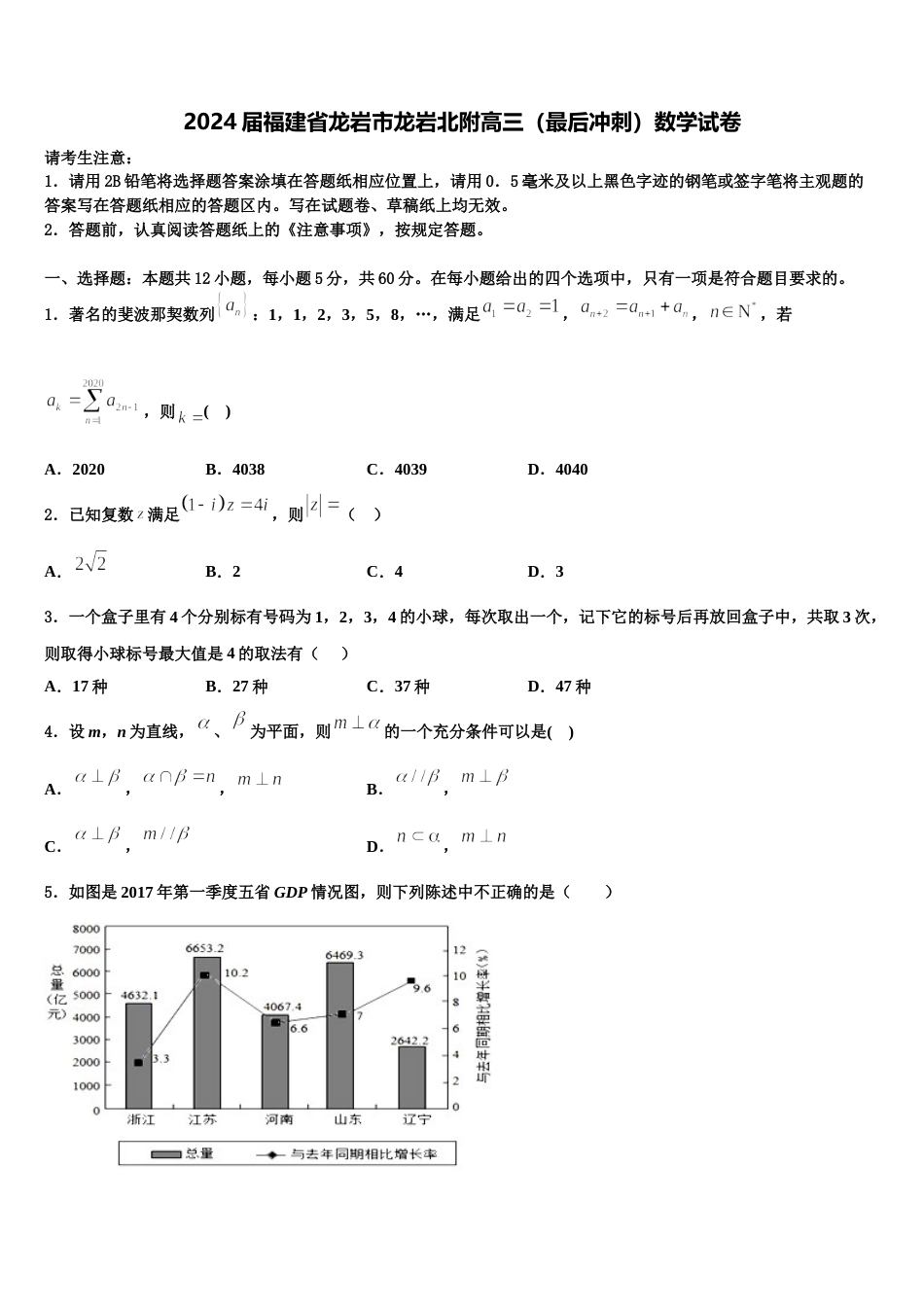
2024 届福建省龙岩市龙岩北附高三(最后冲刺)数学试卷请考生注意:1.请用 2B 铅笔将选择题答案涂填在答题纸相应位置上,请用 0.5 毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.著名的斐波那契数列:1,1,2,3,5,8,…,满足,,,若,则( )A.2020B.4038C.4039D.40402.已知复数满足,则( )A.B.2C.4D.33.一个盒子里有 4 个分别标有号码为 1,2,3,4 的小球,每次取出一个,记下它的标号后再放回盒子中,共取 3 次,则取得小球标号最大值是 4 的取法有( )A.17 种B.27 种C.37 种D.47 种4.设 m,n 为直线,、为平面,则的一个充分条件可以是( )A.,,B.,C.,D.,5.如图是 2017 年第一季度五省 GDP 情况图,则下列陈述中不正确的是( )A.2017 年第一季度 GDP 增速由高到低排位第 5 的是浙江省.B.与去年同期相比,2017 年第一季度的 GDP 总量实现了增长.C.2017 年第一季度 GDP 总量和增速由高到低排位均居同一位的省只有 1 个D.去年同期河南省的 GDP 总量不超过 4000 亿元.6.已知数列满足:)若正整数使得成立,则( )A.16B.17C.18D.197.已知函数.设,若对任意不相等的正数,,恒有,则实数 a 的取值范围是( )A.B.C.D.8.在空间直角坐标系中,四面体各顶点坐标分别为:.假设蚂蚁窝在点,一只蚂蚁从点出发,需要在,上分别任意选择一点留下信息,然后再返回点.那么完成这个工作所需要走的最短路径长度是( )A.B.C.D.9.已知椭圆(a>b>0)与双曲线(a>0,b>0)的焦点相同,则双曲线渐近线方程为()A.B.C.D.10.设双曲线(a>0,b>0)的一个焦点为 F(c,0)(c>0),且离心率等于,若该双曲线的一条渐近线被圆 x2+y22﹣ cx=0 截得的弦长为 2,则该双曲线的标准方程为( )A.B.C.D.11.已知函数,若函数的所有零点依次记为,且,则( )A.B.C.D.12.设 是虚数单位,复数( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知函数,若方程的解为,(),则_______;_______.14.已知半径为 4 的球面上有两点,,球心为 O,若球面上的动点 C 满足二面角的大小为,则四面体的外接球的半径为_________.15.某中学数学竞赛培训班共有 10 人,分为甲、乙两个小组,在一次阶段测试中两个小组成绩的茎叶图如图所示,若甲组 5 名同学成绩的平均数为 81,乙组 5 名同学成绩的中位数为 73,则 x- y 的值为________.16.在一底面半径和高都是的圆柱形容器中盛满小麦,有一粒带麦锈病的种子混入了其中.现从中随机取出的种子,则取出了带麦锈病种子的概率是_____.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知函数.(1)讨论的零点个数;(2)证明:当时,.18.(12 分)已知函数的定义域为,且满足,当时,有,且.(1)求不等式的解集;(2)对任意,恒成立,求实数的取值范围.19.(12 分)如图,在四棱柱中,底面为菱形,.(1)证明:平面平面;(2)若,是等边三角形,求二面角的余弦值.20.(12 分)数列的前项和为,且.数列满足,其前项和为.(1)求数列与的通项公式;(2)设,求数列的前项和.21.(12 分)已知是公比为的无穷等比数列,其前项和为,满足,________.是否存在正整数,使得?若存在,求的最小值;若不存在,说明理由.从①,②,③这三个条件中任选一个,补充在上面问题中并作答.22.(10 分)在如图所示的几何体中,面 CDEF 为正方形,平面 ABCD 为等腰梯形,AB//CD,AB =2BC,点 Q 为AE 的中点.(1)求证:AC//平面 DQF;(2)若∠ABC=60°,AC⊥FB,求 BC 与平面 DQF 所成角的正弦值.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选...