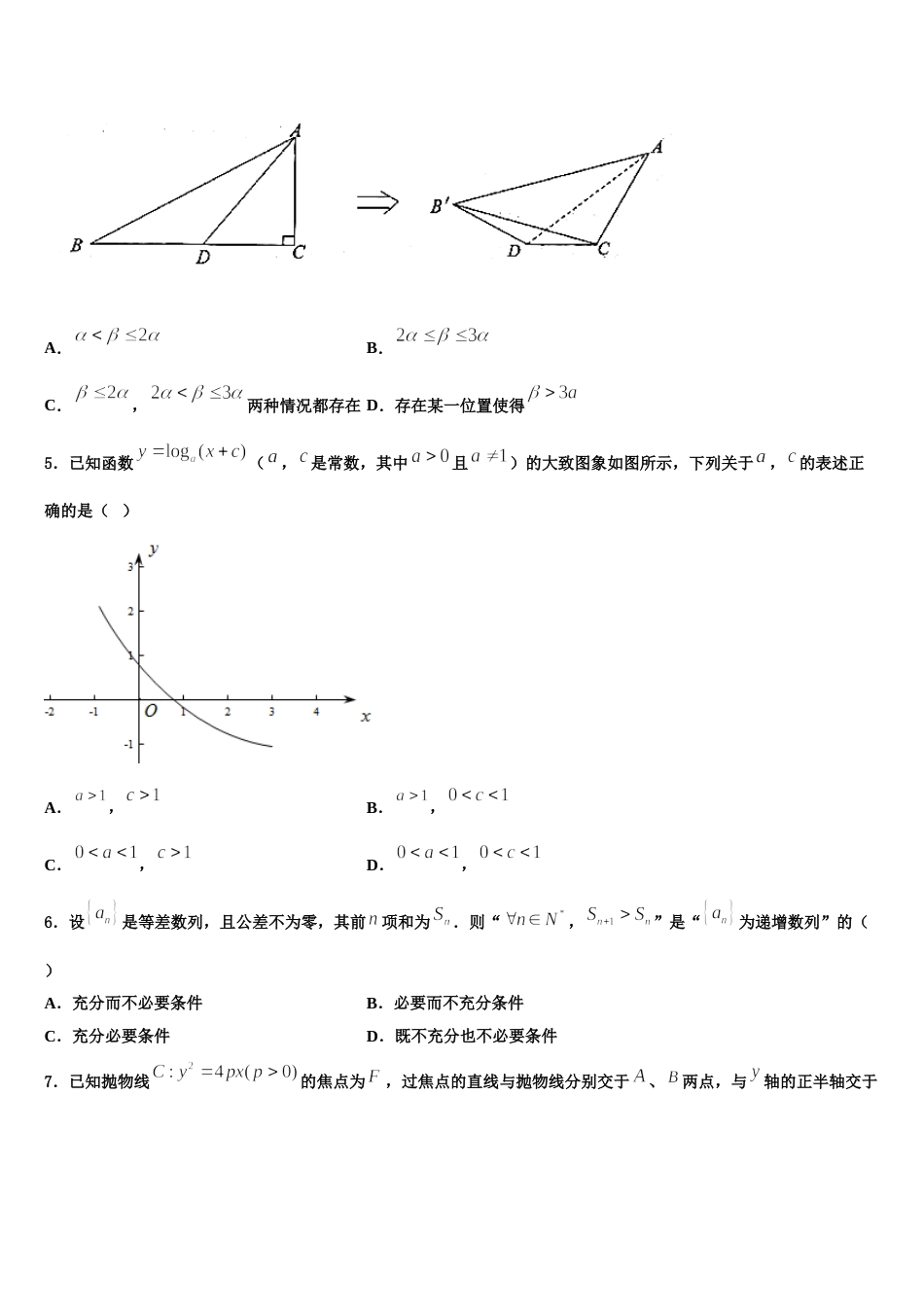
2024 届西安市第二十六中学高考数学押题试卷请考生注意:1.请用 2B 铅笔将选择题答案涂填在答题纸相应位置上,请用 0.5 毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.盒中有 6 个小球,其中 4 个白球,2 个黑球,从中任取个球,在取出的球中,黑球放回,白球则涂黑后放回,此时盒中黑球的个数,则( )A.,B.,C.,D.,2.已知甲、乙两人独立出行,各租用共享单车一次(假定费用只可能为 、 、 元).甲、乙租车费用为 元的概率分别是、,甲、乙租车费用为元的概率分别是、,则甲、乙两人所扣租车费用相同的概率为( )A.B.C.D.3.若,,,点 C 在 AB 上,且,设,则的值为( )A.B.C.D.4.如图,中,点 D 在 BC 上,,将沿 AD 旋转得到三棱锥,分别记,与平面 ADC 所成角为,,则,的大小关系是( )A.B.C.,两种情况都存在 D.存在某一位置使得5.已知函数(,是常数,其中且)的大致图象如图所示,下列关于,的表述正确的是( )A.,B.,C.,D.,6.设是等差数列,且公差不为零,其前项和为.则“,”是“为递增数列”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件7.已知抛物线的焦点为,过焦点的直线与抛物线分别交于、两点,与轴的正半轴交于点,与准线 交于点,且,则( )A.B.2C.D.38.若复数满足,其中 为虚数单位,是的共轭复数,则复数( )A.B.C.4D.59.已知等差数列中,,则( )A.20B.18C.16D.1410.已知椭圆:的左、右焦点分别为,,过的直线与轴交于点,线段与交于点.若,则的方程为( )A.B.C.D.11.已知函数,则不等式的解集为( )A.B.C.D.12.已知函数,的图象与直线的两个相邻交点的距离等于,则的一条对称轴是( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.函数的定义域为__________.14.在中,内角的对边分别是,若,,则____.15.在数列中,,则数列的通项公式_____.16.复数为虚数单位)的虚部为__________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知函数存在一个极大值点和一个极小值点.(1)求实数 a 的取值范围;(2)若函数的极大值点和极小值点分别为和,且,求实数 a 的取值范围.(e 是自然对数的底数)18.(12 分)如图,四棱锥中,底面为直角梯形,∥,为等边三角形,平面底面,为的中点. (1)求证:平面平面;(2)点在线段上,且,求平面与平面所成的锐二面角的余弦值.19.(12 分)已知矩阵,二阶矩阵满足.(1)求矩阵;(2)求矩阵的特征值.20.(12 分)已知三棱锥中侧面与底面都是边长为 2 的等边三角形,且面面,分别为线段的中点.为线段上的点,且.(1)证明:为线段的中点;(2)求二面角的余弦值.21.(12 分)若函数为奇函数,且时有极小值.(1)求实数的值与实数的取值范围;(2)若恒成立,求实数的取值范围.22.(10 分)已知曲线的参数方程为(为参数),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为.(1)写出曲线的极坐标方程;(2)点是曲线上的一点,试判断点与曲线的位置关系.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、C【解析】根据古典概型概率计算公式,计算出概率并求得数学期望,由此判断出正确选项.【详解】表示取出的为一个白球,所以.表示取出一个黑球,,所以.表示取出两个球,其中一黑一白,,表示取出两个球为黑球,,表示取出两个球为白球,,所以.所以,.故选:C【点睛】本小题主要考查离散型随机变量分布列和数学期望的计算,属于中档题.2、B【解析】甲、乙两人所扣租车费用相同即同为 1 元,或同为 2 元,或同为 3 元,...