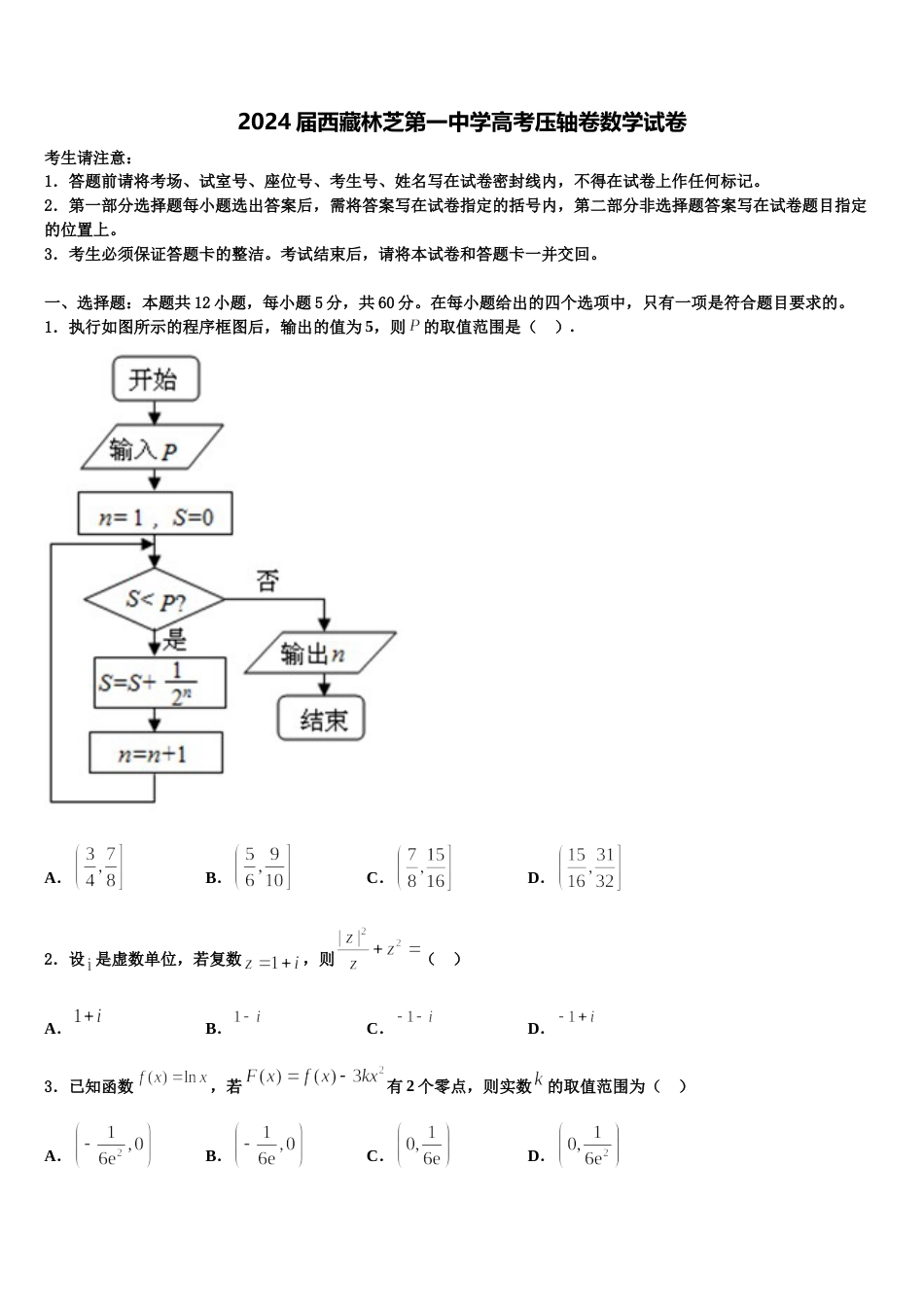
2024 届西藏林芝第一中学高考压轴卷数学试卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.执行如图所示的程序框图后,输出的值为 5,则的取值范围是( ). A.B.C.D.2.设 是虚数单位,若复数,则( )A.B.C.D.3.已知函数,若有 2 个零点,则实数的取值范围为( )A.B.C.D.4.设 M 是边 BC 上任意一点,N 为 AM 的中点,若,则的值为( )A.1B.C.D.5.已知平行于轴的直线分别交曲线于两点,则的最小值为( )A.B.C.D.6.圆柱被一平面截去一部分所得几何体的三视图如图所示,则该几何体的体积为( ) A.B.C.D.7.已知集合,集合,则( )A.B.C.D.8.已知函数,则在上不单调的一个充分不必要条件可以是( )A.B.C.或D.9.已知全集,集合,,则( )A.B.C.D.10.函数在上的最大值和最小值分别为( )A.,-2B.,-9C.-2,-9D.2,-211.斜率为 1 的直线 l 与椭圆相交于 A、B 两点,则的最大值为 A.2B.C.D.12.国务院发布《关于进一步调整优化结构、提高教育经费使用效益的意见》中提出,要优先落实教育投入.某研究机构统计了年至年国家财政性教育经费投入情况及其在中的占比数据,并将其绘制成下表,由下表可知下列叙述错误的是( )A.随着文化教育重视程度的不断提高,国在财政性教育经费的支出持续增长B.年以来,国家财政性教育经费的支出占比例持续年保持在以上C.从年至年,中国的总值最少增加万亿D.从年到年,国家财政性教育经费的支出增长最多的年份是年二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.的角所对的边分别为,且,,若,则的值为__________.14.若的展开式中各项系数之和为 32,则展开式中 x 的系数为_____15.将一颗质地均匀的正方体骰子(每个面上分别写有数字 1,2,3,4,5,6)先后抛掷 2 次,观察向上的点数,则点数之和是 6 的的概率是___.16.如图,在菱形 ABCD 中,AB=3,,E,F 分别为 BC,CD 上的点,,若线段 EF上存在一点 M,使得,则____________,____________.(本题第 1 空 2 分,第 2 空 3 分)三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)在直角坐标系中,已知点,若以线段为直径的圆与轴相切.(1)求点的轨迹的方程;(2)若上存在两动点(A,B 在轴异侧)满足,且的周长为,求的值.18.(12 分)某职称晋级评定机构对参加某次专业技术考试的 100 人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定 80 分及以上者晋级成功,否则晋级失败.晋级成功晋级失败合计男16女50合计(1)求图中的值;(2)根据已知条件完成下面列联表,并判断能否有的把握认为“晋级成功”与性别有关?(3)将频率视为概率,从本次考试的所有人员中,随机抽取 4 人进行约谈,记这 4 人中晋级失败的人数为,求的分布列与数学期望.(参考公式:,其中)0.400.250.150.100.050.0250.7801.3232.0722.7063.8415.02419.(12 分)已知命题:,;命题:函数无零点.(1)若为假,求实数的取值范围;(2)若为假,为真,求实数的取值范围.20.(12 分)选修 4—5;不等式选讲.已知函数.(1)若的解集非空,求实数的取值范围;(2)若正数满足,为(1)中 m 可取到的最大值,求证:.21.(12 分)已知函数,.(1)讨论函数的单调性;(2)已知在处的切线与轴垂直,若方程有三个实数解、、(),求证:.22.(10 分)管道清洁棒是通过在管道内释放清洁剂来清洁管道内壁的工具,现欲用清洁棒清洁一个如图 1 所示的圆管直角弯头的内壁,其纵截面如图 2 所示,一根长度为的清洁棒在弯头内恰好处于位置(图中给...