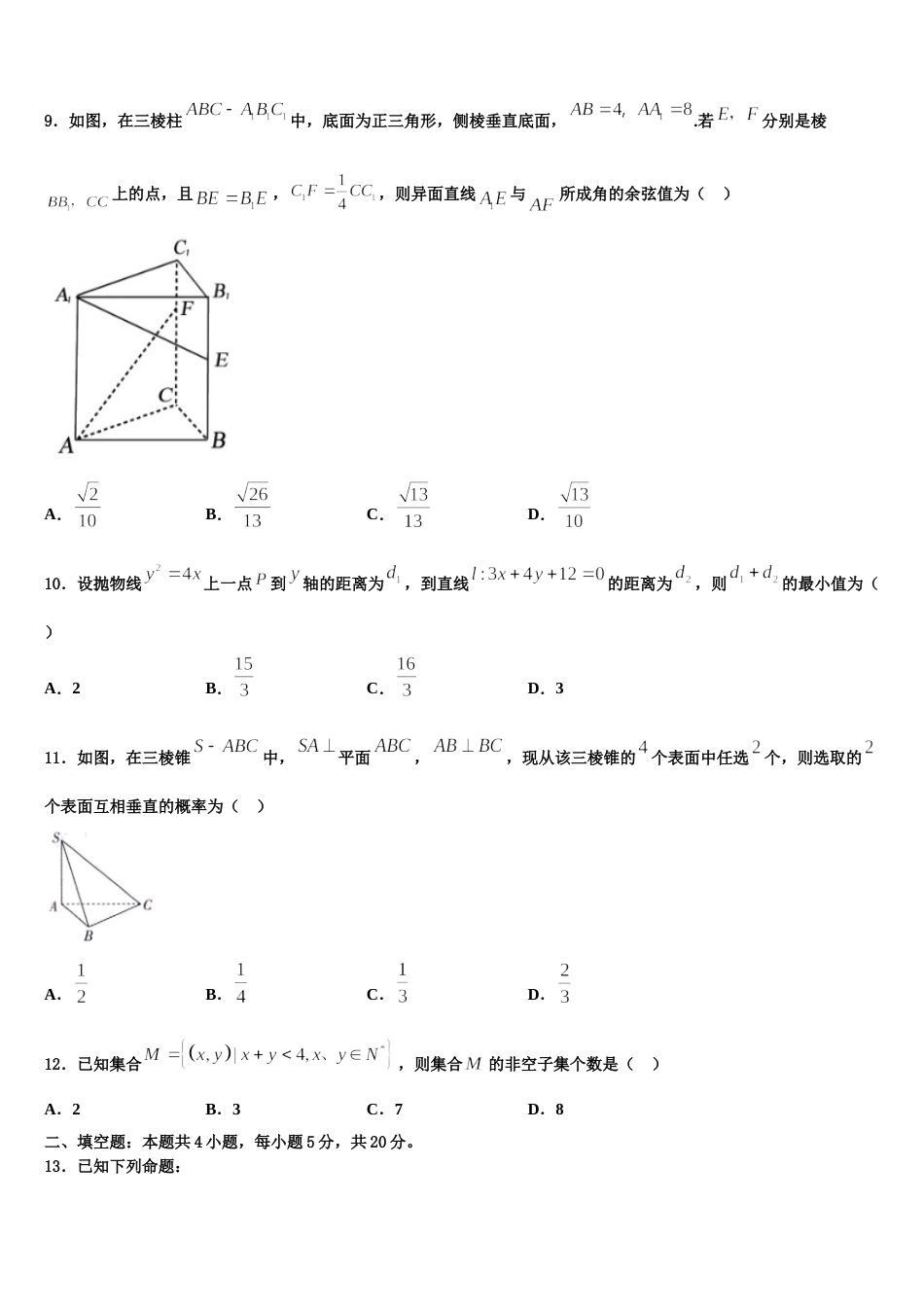
2024 届赣湘粤三省六校高考全国统考预测密卷数学试卷注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用 2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.如图所示,矩形的对角线相交于点,为的中点,若,则等于( ).A.B.C.D.2.已知函数 f(x)=sin2x+sin2(x),则 f(x)的最小值为( )A.B.C.D.3.已知是空间中两个不同的平面,是空间中两条不同的直线,则下列说法正确的是( )A.若,且,则B.若,且,则C.若,且,则D.若,且,则4.已知等差数列{an},则“a2>a1”是“数列{an}为单调递增数列”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件5.若双曲线:()的一个焦点为,过点的直线 与双曲线交于、两点,且的中点为,则的方程为( )A.B.C.D.6.已知为圆:上任意一点,,若线段的垂直平分线交直线于点,则点的轨迹方程为( )A.B.C.()D.()7.已知函数(,,),将函数的图象向左平移个单位长度,得到函数的部分图象如图所示,则是的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件8.是的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件9.如图,在三棱柱中,底面为正三角形,侧棱垂直底面,.若分别是棱上的点,且,,则异面直线与所成角的余弦值为( )A.B.C.D.10.设抛物线上一点到轴的距离为,到直线的距离为,则的最小值为()A.2B.C.D.311.如图,在三棱锥中,平面,,现从该三棱锥的个表面中任选个,则选取的个表面互相垂直的概率为( )A.B.C.D.12.已知集合,则集合的非空子集个数是( )A.2B.3C.7D.8二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知下列命题:① 命题“∃x0R∈ ,”的否定是“∀xR∈ ,x2+1<3x”;② 已知 p,q 为两个命题,若“p∨q”为假命题,则“”为真命题;“③ a>2”是“a>5”的充分不必要条件;“④ 若 xy=0,则 x=0 且 y=0”的逆否命题为真命题.其中所有真命题的序号是________.14.函数在区间内有且仅有两个零点,则实数的取值范围是_____.15.给出下列四个命题,其中正确命题的序号是_____.(写出所有正确命题的序号)因为所以不是函数的周期;对于定义在上的函数若则函数不是偶函数;“”是“”成立的充分必要条件;若实数满足则.16.已知向量,,则______.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)如图在四边形中,,,为中点,.(1)求;(2)若,求面积的最大值.18.(12 分)已知数列满足:对一切成立.(1)求数列的通项公式;(2)求数列的前项和.19.(12 分)某大学开学期间,该大学附近一家快餐店招聘外卖骑手,该快餐店提供了两种日工资结算方案:方案规定每日底薪 100 元,外卖业务每完成一单提成 2 元;方案规定每日底薪 150 元,外卖业务的前 54 单没有提成,从第 55 单开始,每完成一单提成 5 元.该快餐店记录了每天骑手的人均业务量,现随机抽取 100 天的数据,将样本数据分为七组,整理得到如图所示的频率分布直方图.(1)随机选取一天,估计这一天该快餐店的骑手的人均日外卖业务量不少于 65 单的概率;(2)从以往统计数据看,新聘骑手选择日工资方案的概率为,选择方案的概率为.若甲、乙、丙、丁四名骑手分别到该快餐店应聘,四人选择日工资方案相互独立,求至少有两名骑手选择方案的概率,(3)若仅从人日均收入的角度考虑,请你为新聘骑手做出日工资方案的选择,并说明理由.(同组中的每个数据用该组区间的中点值代替)20.(12 分)已知各项均为正数的数列的前项和为,且是与的等差中项.(1)证明:为等差数列,并求;(2)设,数列的前项和为,求满足的最小正整数的值.21.(...