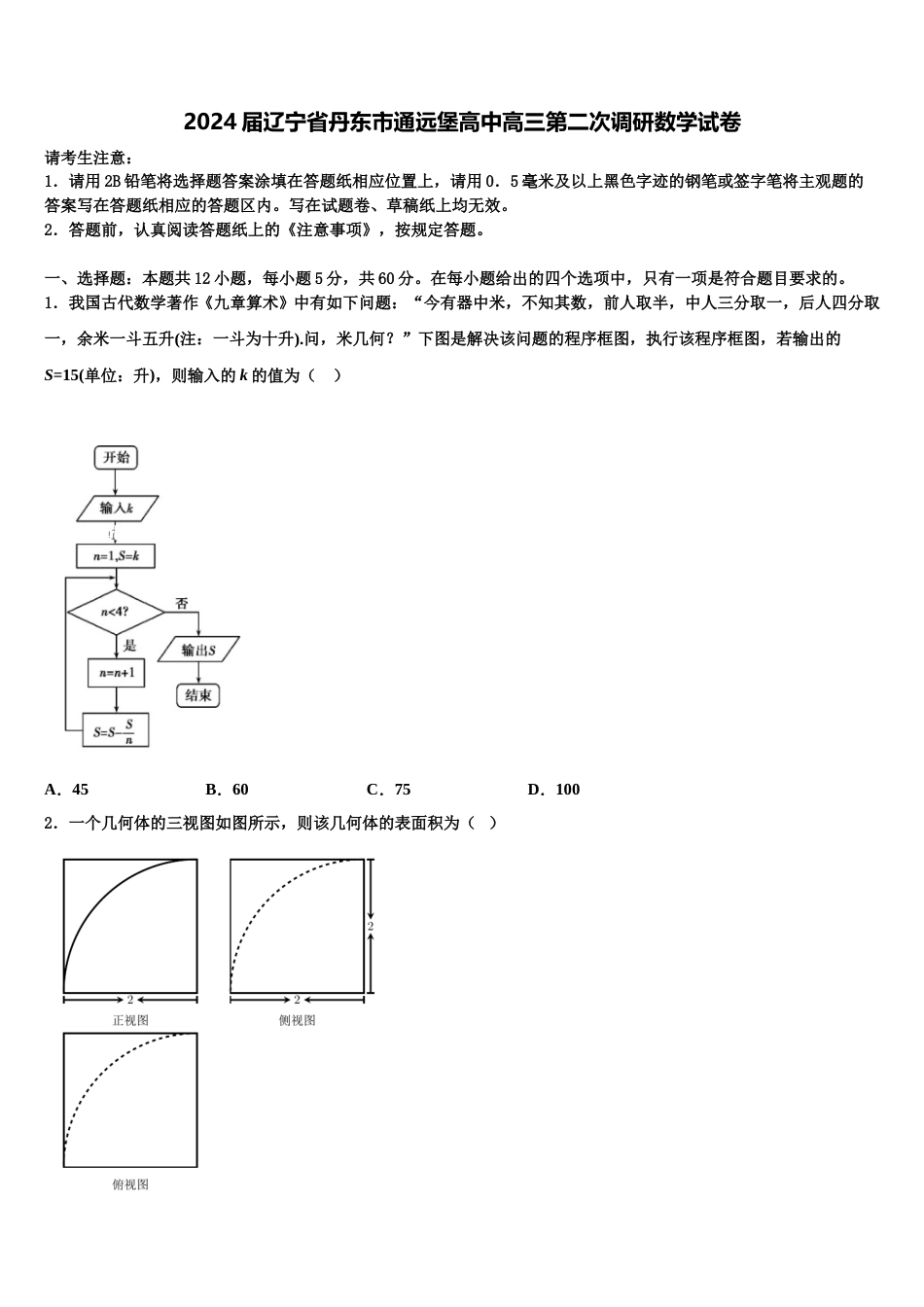
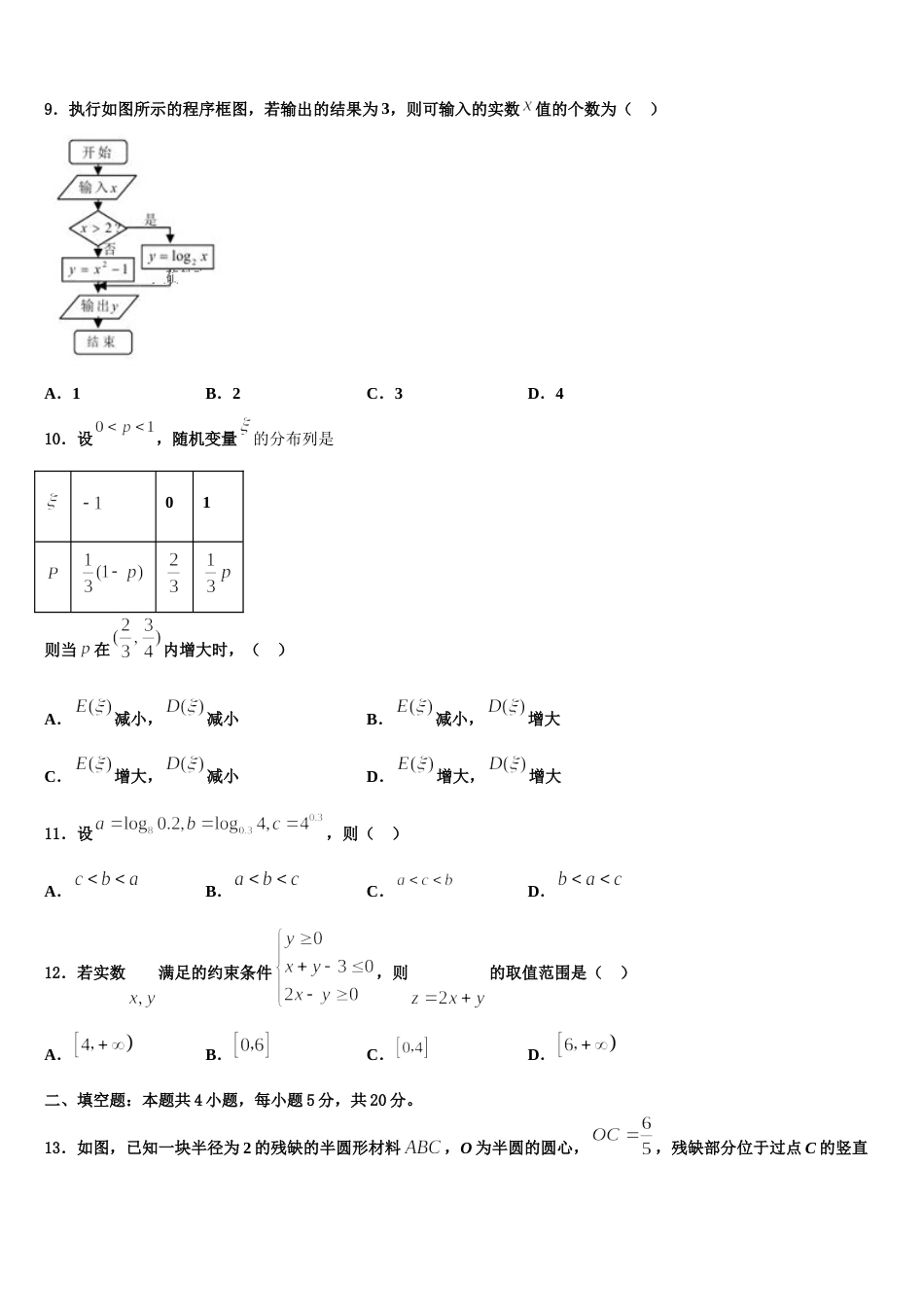
2024 届辽宁省丹东市通远堡高中高三第二次调研数学试卷请考生注意:1.请用 2B 铅笔将选择题答案涂填在答题纸相应位置上,请用 0.5 毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.我国古代数学著作《九章算术》中有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升(注:一斗为十升).问,米几何?”下图是解决该问题的程序框图,执行该程序框图,若输出的S=15(单位:升),则输入的 k 的值为( ) A.45B.60C.75D.1002.一个几何体的三视图如图所示,则该几何体的表面积为( )A.B.C.D.3.已知为锐角,且,则等于( )A.B.C.D.4.一个陶瓷圆盘的半径为,中间有一个边长为的正方形花纹,向盘中投入 1000 粒米后,发现落在正方形花纹上的米共有 51 粒,据此估计圆周率的值为(精确到 0.001)( )A.3.132B.3.137C.3.142D.3.1475.我国古代数学名著《九章算术》有一问题:“今有鳖臑(biē naò),下广五尺,无袤;上袤四尺,无广;高七尺.问积几何?”该几何体的三视图如图所示,则此几何体外接球的表面积为( )A.平方尺B.平方尺C.平方尺D.平方尺6.设分别为的三边的中点,则( )A.B.C.D.7.下列函数中,值域为 R 且为奇函数的是( )A.B.C.D.8.设,满足,则的取值范围是( )A.B.C.D.9.执行如图所示的程序框图,若输出的结果为 3,则可输入的实数值的个数为( )A.1B.2C.3D.410.设,随机变量的分布列是01则当在内增大时,( )A.减小,减小B.减小,增大C.增大,减小D.增大,增大11.设,则( )A.B.C.D.12.若实数满足的约束条件,则的取值范围是( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.如图,已知一块半径为 2 的残缺的半圆形材料,O 为半圆的圆心,,残缺部分位于过点 C 的竖直线的右侧,现要在这块材料上裁出一个直角三角形,若该直角三角形一条边在上,则裁出三角形面积的最大值为______.14.在四面体中,与都是边长为 2 的等边三角形,且平面平面,则该四面体外接球的体积为_______.15.在二项式的展开式中,的系数为________.16.如图,直线 是曲线在处的切线,则________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知函数(I)若讨论的单调性;(Ⅱ)若,且对于函数的图象上两点,存在,使得函数的图象在处的切线.求证:.18.(12 分)已知函数,.(1)求函数在处的切线方程;(2)当时,证明:对任意恒成立.19.(12 分)在平面直角坐标系中,已知点,曲线:(为参数)以原点为极点,轴正半轴建立极坐标系,直线 的极坐标方程为.(Ⅰ)判断点与直线 的位置关系并说明理由;(Ⅱ)设直线与曲线的两个交点分别为,,求的值.20.(12 分)如图,在平面直角坐标系中,椭圆的离心率为,且过点.求椭圆的方程;已知是椭圆的内接三角形,① 若点为椭圆的上顶点,原点为的垂心,求线段的长;② 若原点为的重心,求原点到直线距离的最小值.21.(12 分)已知数列是各项均为正数的等比数列,数列为等差数列,且,,.(1)求数列与的通项公式;(2)求数列的前项和;(3)设为数列的前项和,若对于任意,有,求实数 的值.22.(10 分)如图,在中,已知,,,为线段的中点,是由绕直线旋转而成,记二面角的大小为.(1)当平面平面时,求的值;(2)当时,求二面角的余弦值.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、B【解析】根据程序框图中程序的功能,可以列方程计算.【详解】由题意,.故选:B.【点睛】本题考查程序框图,读懂程序的功能是解题关键.2、B【解析】由题意首先确定几何体的空间结构特征,然后结合空间结构特征即可求得...