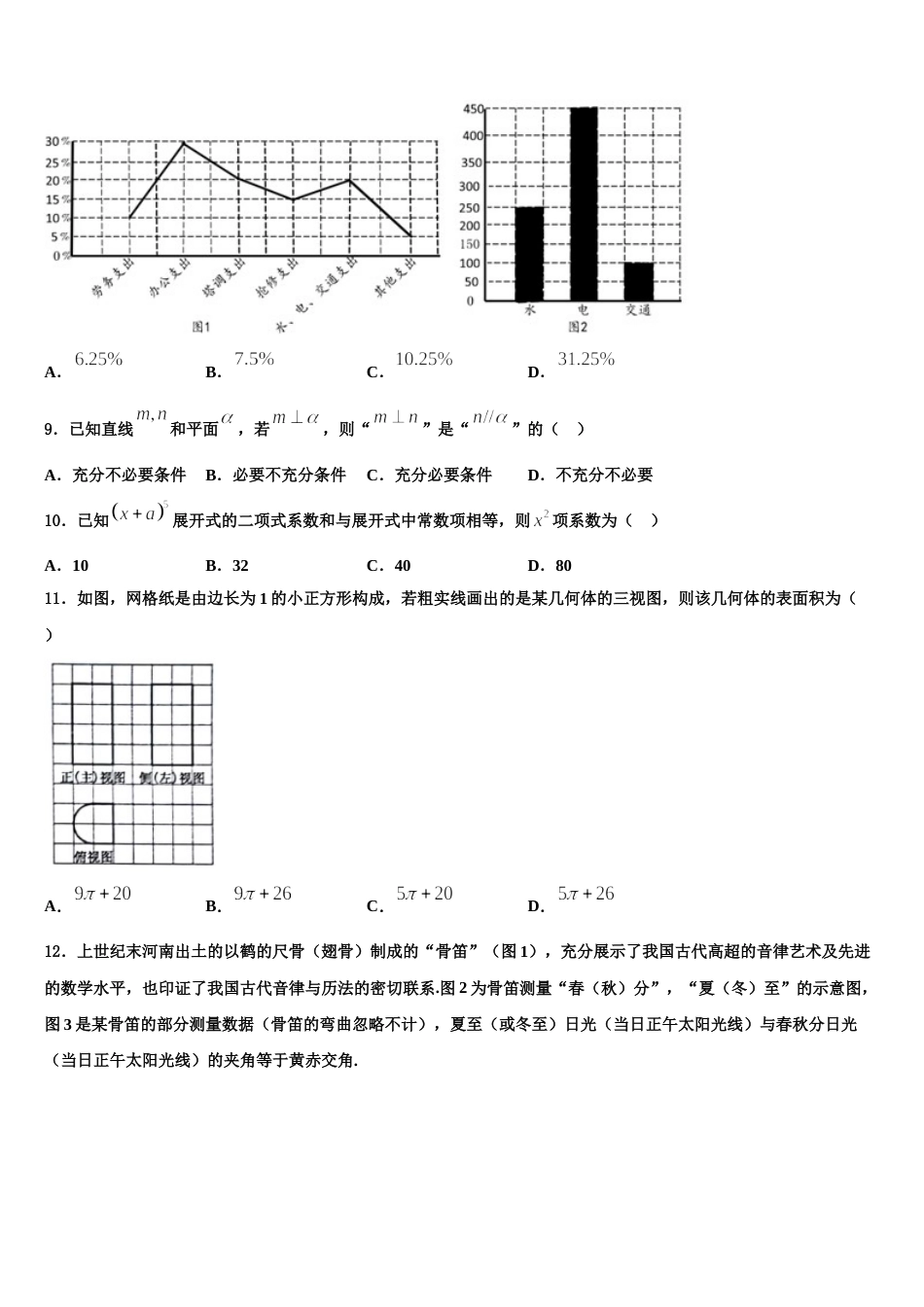
2024 届辽宁省五校联考(省实验,育才中学高三下第一次测试数学试题注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知双曲线:(,)的右焦点与圆:的圆心重合,且圆被双曲线的一条渐近线截得的弦长为,则双曲线的离心率为( )A.2B.C.D.32.在很多地铁的车厢里,顶部的扶手是一根漂亮的弯管,如下图所示.将弯管形状近似地看成是圆弧,已知弯管向外的最大突出(图中)有,跨接了 6 个坐位的宽度(),每个座位宽度为,估计弯管的长度,下面的结果中最接近真实值的是( )A.B.C.D.3.已知函数在区间上恰有四个不同的零点,则实数的取值范围是( )A.B.C.D.4.甲、乙、丙、丁四位同学利用暑假游玩某风景名胜大峡谷,四人各自去景区的百里绝壁、千丈瀑布、原始森林、远古村寨四大景点中的一个,每个景点去一人.已知:①甲不在远古村寨,也不在百里绝壁;②乙不在原始森林,也不在远古村寨;③“丙在远古村寨”是“甲在原始森林”的充分条件;④丁不在百里绝壁,也不在远古村寨.若以上语句都正确,则游玩千丈瀑布景点的同学是( )A.甲B.乙C.丙D.丁5.( )A.B.C.D.6.为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度.某地区在 2015 年以前的年均脱贫率(脱离贫困的户数占当年贫困户总数的比)为.2015 年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中 2019 年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:实施项目种植业养殖业工厂就业服务业参加用户比脱贫率那么年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )A.倍B.倍C.倍D.倍7.刘徽(约公元 225 年-295 年),魏晋期间伟大的数学家,中国古典数学理论的奠基人之一他在割圆术中提出的,“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,这可视为中国古代极限观念的佳作,割圆术的核心思想是将一个圆的内接正 n 边形等分成 n 个等腰三角形(如图所示),当 n 变得很大时,这 n 个等腰三角形的面积之和近似等于圆的面积,运用割圆术的思想,得到的近似值为( )A.B.C.D.8.某单位去年的开支分布的折线图如图 1 所示,在这一年中的水、电、交通开支(单位:万元)如图 2 所示,则该单位去年的水费开支占总开支的百分比为( )A.B.C.D.9.已知直线和平面,若,则“”是“”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.不充分不必要10.已知展开式的二项式系数和与展开式中常数项相等,则项系数为( )A.10B.32C.40D.8011.如图,网格纸是由边长为 1 的小正方形构成,若粗实线画出的是某几何体的三视图,则该几何体的表面积为( )A.B.C.D.12.上世纪末河南出土的以鹤的尺骨(翅骨)制成的“骨笛”(图 1),充分展示了我国古代高超的音律艺术及先进的数学水平,也印证了我国古代音律与历法的密切联系.图 2 为骨笛测量“春(秋)分”,“夏(冬)至”的示意图,图 3 是某骨笛的部分测量数据(骨笛的弯曲忽略不计),夏至(或冬至)日光(当日正午太阳光线)与春秋分日光(当日正午太阳光线)的夹角等于黄赤交角.由历法理论知,黄赤交角近 1 万年持续减小,其正切值及对应的年代如下表:黄赤交角正切值0.4390.4440.4500.4550.461年代公元元年公元前 2000 年公元前 4000 年公元前 6000 年公元前 8000 年根据以上信息,通过计算黄赤交角,可估计该骨笛的大致年代是( )A.公元前 2000 年到公元元年B.公元前 4000 年到公元前 2000 年C.公元前 6000 年到公元前 4000 年D.早于公元前 6000 年二、...