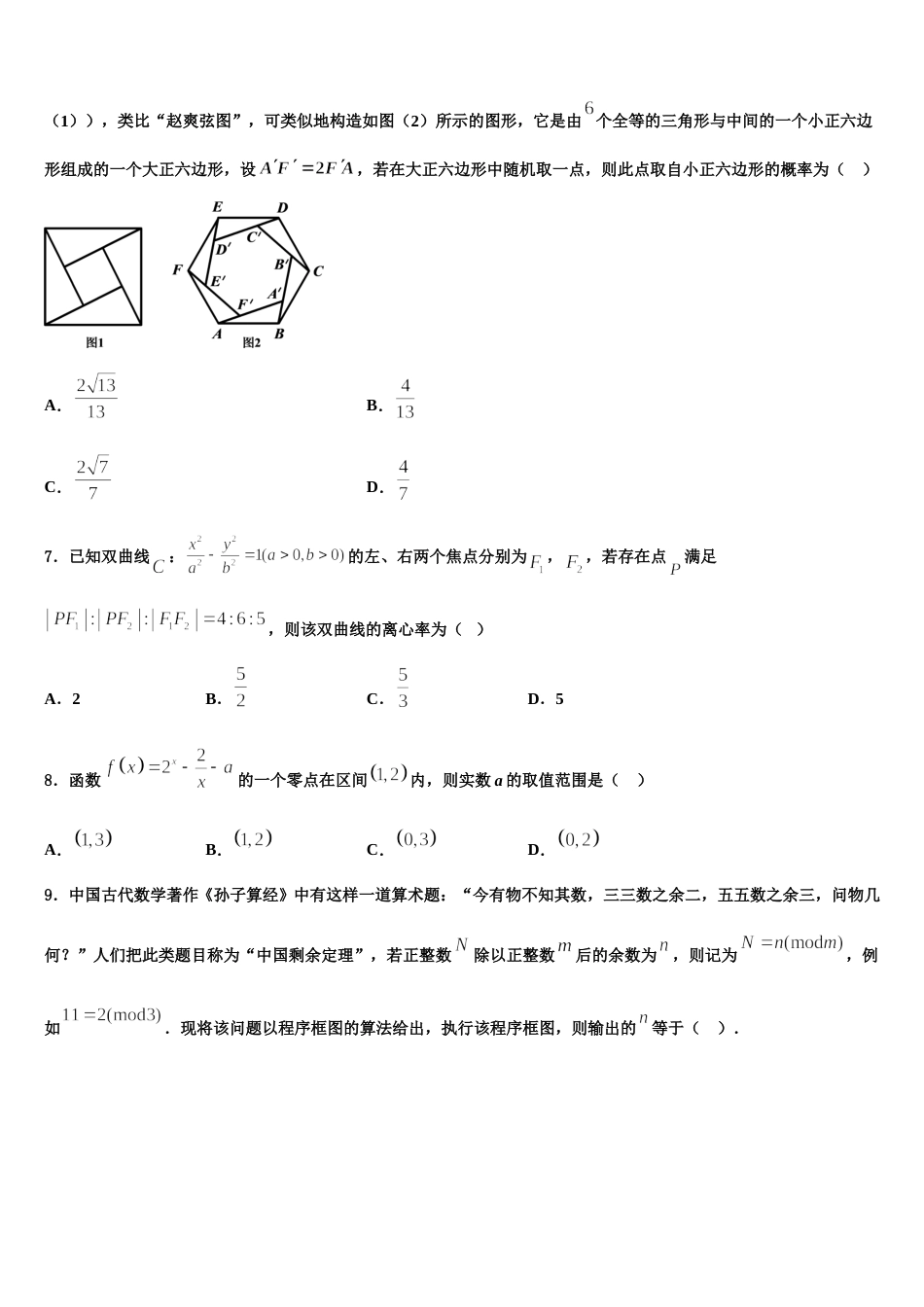
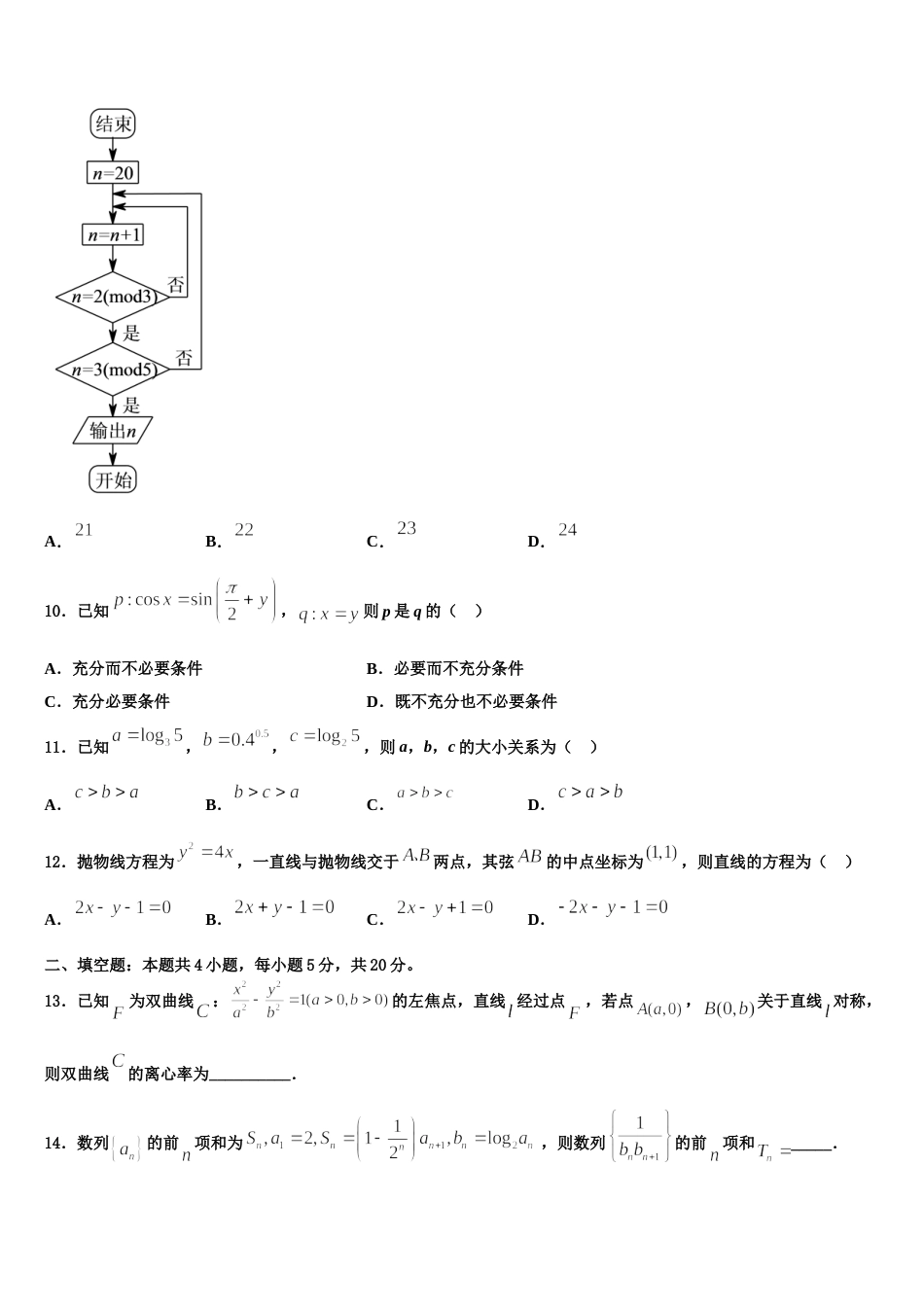
2024 届辽宁省大石桥市第二高级中学高考仿真卷数学试题注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。2.选择题必须使用 2B 铅笔填涂;非选择题必须使用 0.5 毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.设复数,则=( )A.1B.C.D.2.设是两条不同的直线,是两个不同的平面,下列命题中正确的是( )A.若,,则B.若,,则C.若,,则D.若,,则3.若实数 x,y 满足条件,目标函数,则 z 的最大值为( )A.B.1C.2D.04.下列函数中,值域为 R 且为奇函数的是( )A.B.C.D.5.关于函数,有下列三个结论:①是的一个周期;②在上单调递增;③的值域为.则上述结论中,正确的个数为()A.B.C.D.6.赵爽是我国古代数学家、天文学家,大约公元 222 年,赵爽为《周髀算经》一书作序时,介绍了“勾股圆方图”,又称“赵爽弦图”(以弦为边长得到的正方形是由个全等的直角三角形再加上中间的一个小正方形组成的,如图(1)),类比“赵爽弦图”,可类似地构造如图(2)所示的图形,它是由个全等的三角形与中间的一个小正六边形组成的一个大正六边形,设,若在大正六边形中随机取一点,则此点取自小正六边形的概率为( )A.B.C.D.7.已知双曲线:的左、右两个焦点分别为,,若存在点满足,则该双曲线的离心率为( )A.2B.C.D.58.函数的一个零点在区间内,则实数 a 的取值范围是( )A.B.C.D.9.中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”人们把此类题目称为“中国剩余定理”,若正整数除以正整数后的余数为,则记为,例如.现将该问题以程序框图的算法给出,执行该程序框图,则输出的等于( ).A.B.C.D.10.已知,则 p 是 q 的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件11.已知,,,则 a,b,c 的大小关系为( )A.B.C.D.12.抛物线方程为,一直线与抛物线交于两点,其弦的中点坐标为,则直线的方程为( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知为双曲线:的左焦点,直线 经过点,若点,关于直线 对称,则双曲线的离心率为__________.14.数列的前项和为 ,则数列的前项和_____.15.若实数满足不等式组,则的最小值是___16.设满足约束条件,则目标函数的最小值为_.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)在本题中,我们把具体如下性质的函数叫做区间上的闭函数:①的定义域和值域都是;②在上是增函数或者减函数.(1)若在区间上是闭函数,求常数的值;(2)找出所有形如的函数(都是常数),使其在区间上是闭函数.18.(12 分)如图,四棱锥中,底面为直角梯形,,,,,在锐角中,E 是边 PD 上一点,且.(1)求证:平面 ACE;(2)当 PA 的长为何值时,AC 与平面 PCD 所成的角为?19.(12 分)已知函数,.(1)当时,讨论函数的零点个数;(2)若在上单调递增,且求 c 的最大值.20.(12 分)在一次电视节目的答题游戏中,题型为选择题,只有“A”和“B”两种结果,其中某选手选择正确的概率为 p,选择错误的概率为 q,若选择正确则加 1 分,选择错误则减 1 分,现记“该选手答完 n 道题后总得分为”.(1)当时,记,求的分布列及数学期望;(2)当,时,求且的概率.21.(12 分)已知函数.(1)讨论的单调性;(2)若在定义域内是增函数,且存在不相等的正实数,使得,证明:.22.(10 分)已知,,分别是三个内角,,的对边,.(1)求;(2)若,,求,.参考答案一、选择题:本题共 12 小题,每小题 5 分,...