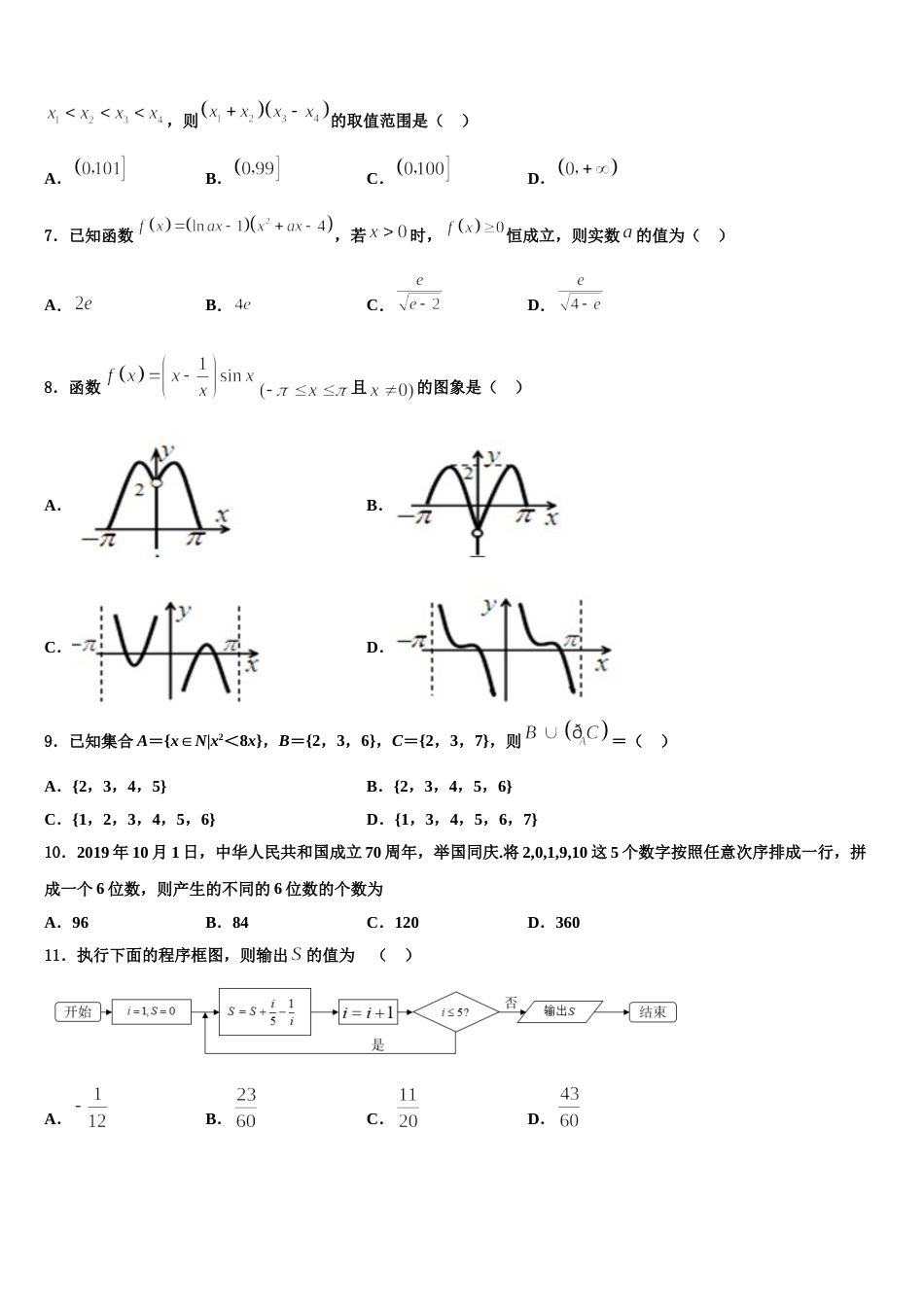
2024 届重庆市九龙坡区高三适应性调研考试数学试题注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用 2B 铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。2.作答选择题时,选出每小题答案后,用 2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试题卷上。3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。不按以上要求作答无效。4.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.把满足条件(1),,(2),,使得的函数称为“D 函数”,下列函数是“D 函数”的个数为( )① ② ③ ④ ⑤A.1 个B.2 个C.3 个D.4 个2.设分别为双曲线的左、右焦点,过点作圆的切线,与双曲线的左、右两支分别交于点,若,则双曲线渐近线的斜率为( )A.B.C.D.3.复数满足为虚数单位),则的虚部为( )A.B.C.D.4.设、是两条不同的直线,、是两个不同的平面,则的一个充分条件是( )A.且B.且C.且D.且5.已知函数,则方程的实数根的个数是( )A.B.C.D.6.设函数若关于的方程有四个实数解,其中,则的取值范围是( )A.B.C.D.7.已知函数,若时,恒成立,则实数的值为( )A.B.C.D.8.函数且的图象是( )A.B.C.D.9.已知集合 A={x∈N|x2<8x},B={2,3,6},C={2,3,7},则=( )A.{2,3,4,5}B.{2,3,4,5,6}C.{1,2,3,4,5,6}D.{1,3,4,5,6,7}10.2019 年 10 月 1 日,中华人民共和国成立 70 周年,举国同庆.将 2,0,1,9,10 这 5 个数字按照任意次序排成一行,拼成一个 6 位数,则产生的不同的 6 位数的个数为A.96B.84C.120D.36011.执行下面的程序框图,则输出的值为 ( )A.B.C.D.12.已知 是虚数单位,则( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.设为正实数,若则的取值范围是__________.14.双曲线的左右顶点为,以为直径作圆,为双曲线右支上不同于顶点的任一点,连接交圆于点,设直线的斜率分别为,若,则_____.15.在平面直角坐标系中,若函数在处的切线与圆存在公共点,则实数的取值范围为_____.16.在的展开式中的系数为,则_______.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)如图,在直三棱柱中,,,为的中点,点在线段上,且平面.(1)求证:;(2)求平面与平面所成二面角的正弦值.18.(12 分)在直角坐标系中,曲线的参数方程为(为参数,以坐标原点为极点,轴的正半轴为极轴,取相同长度单位建立极坐标系,曲线的极坐标方程为.(1)求曲线的极坐标方程和曲线的普通方程;(2)设射线与曲线交于不同于极点的点,与曲线交于不同于极点的点,求线段的长.19.(12 分)中的内角,,的对边分别是,,,若,.(1)求;(2)若,点为边上一点,且,求的面积.20.(12 分)已知中心在原点的椭圆的左焦点为,与轴正半轴交点为,且.(1)求椭圆的标准方程;(2)过点作斜率为、的两条直线分别交于异于点的两点、.证明:当时,直线过定点.21.(12 分)设都是正数,且,.求证:.22.(10 分)为迎接 2022 年冬奥会,北京市组织中学生开展冰雪运动的培训活动,并在培训结束后对学生进行了考核.记表示学生的考核成绩,并规定为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了 30 名学生的考核成绩,并作成如下茎叶图:(Ⅰ)从参加培训的学生中随机选取 1 人,请根据图中数据,估计这名学生考核优秀的概率;(Ⅱ)从图中考核成绩满足的学生中任取 2 人,求至少有一人考核优秀的概率;(Ⅲ)记表示学生的考核成绩在区间的概率,根据以往培训...