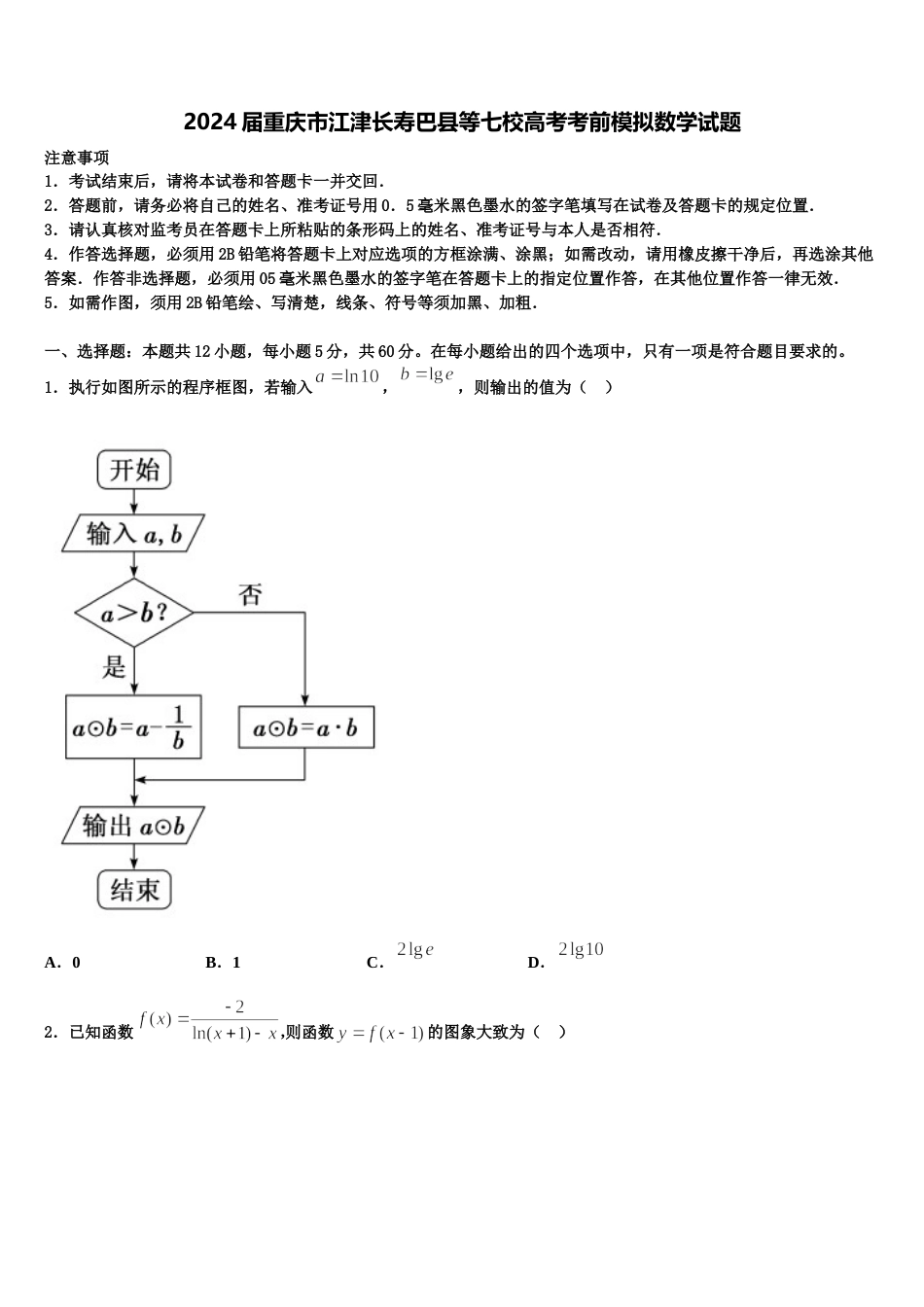
2024 届重庆市江津长寿巴县等七校高考考前模拟数学试题注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用 0.5 毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用 2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用 05 毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用 2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.执行如图所示的程序框图,若输入,,则输出的值为( )A.0B.1C.D.2.已知函数,则函数的图象大致为( )A.B.C.D.3.从某市的中学生中随机调查了部分男生,获得了他们的身高数据,整理得到如下频率分布直方图:根据频率分布直方图,可知这部分男生的身高的中位数的估计值为A.B.C.D.4.已知是定义是上的奇函数,满足,当时, ,则函数在区间上的零点个数是( )A.3B.5C.7D.95.已知,若方程有唯一解,则实数的取值范围是( )A.B.C.D.6.设 m,n 为直线,、为平面,则的一个充分条件可以是( )A.,,B.,C.,D.,7.已知平行于轴的直线分别交曲线于两点,则的最小值为( )A.B.C.D.8.若表示不超过的最大整数(如,,),已知,,,则( )A.2B.5C.7D.89.已知 是虚数单位,若,,则实数( )A.或B.-1 或 1C.1D.10.过双曲线 的左焦点作直线交双曲线的两天渐近线于,两点,若为线段的中点,且(为坐标原点),则双曲线的离心率为( )A.B.C.D.11.设双曲线(a>0,b>0)的右焦点为 F,右顶点为 A,过 F 作 AF 的垂线与双曲线交于 B,C 两点,过 B,C分别作 AC,AB 的垂线交于点 D.若 D 到直线 BC 的距离小于,则该双曲线的渐近线斜率的取值范围是( )A.B.C.D.12.若不相等的非零实数,,成等差数列,且,,成等比数列,则( )A.B.C.2D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知直角坐标系中起点为坐标原点的向量满足,且,,,存在,对于任意的实数,不等式,则实数的取值范围是______.14.已知两个单位向量满足,则向量与的夹角为_____________.15.已知向量,,且,则实数 m 的值是________.16.曲线在点处的切线方程为________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)如图,湖中有一个半径为 千米的圆形小岛,岸边点与小岛圆心相距千米,为方便游人到小岛观光,从点向小岛建三段栈道,,,湖面上的点在线段上,且,均与圆相切,切点分别为,,其中栈道,,和小岛在同一个平面上.沿圆的优弧(圆上实线部分)上再修建栈道.记为.用表示栈道的总长度,并确定的取值范围;求当为何值时,栈道总长度最短.18.(12 分)已知为等差数列,为等比数列,的前 n 项和为,满足,,,.(1)求数列和的通项公式;(2)令,数列的前 n 项和,求.19.(12 分)某贫困地区几个丘陵的外围有两条相互垂直的直线型公路,以及铁路线上的一条应开凿的直线穿山隧道,为进一步改善山区的交通现状,计划修建一条连接两条公路和山区边界的直线型公路 , 以所在的直线分别为轴,轴, 建立平面直角坐标系, 如图所示, 山区边界曲线为,设公路 与曲线相切于点,的横坐标为 .(1)当 为何值时,公路 的长度最短?求出最短长度;(2)当公路 的长度最短时,设公路 交轴,轴分别为,两点,并测得四边形中,,,千米,千米,求应开凿的隧道的长度.20.(12 分)金秋九月,丹桂飘香,某高校迎来了一大批优秀的学生.新生接待其实也是和社会沟通的一个平台.校团委、学生会从在校学生中随机抽取了 160 名学生,对是否愿意投入到新生接待工作进行了问卷调查,统计数据如下:愿意不愿意男生6020女士4040(1)根据上表说明,能否有 9...