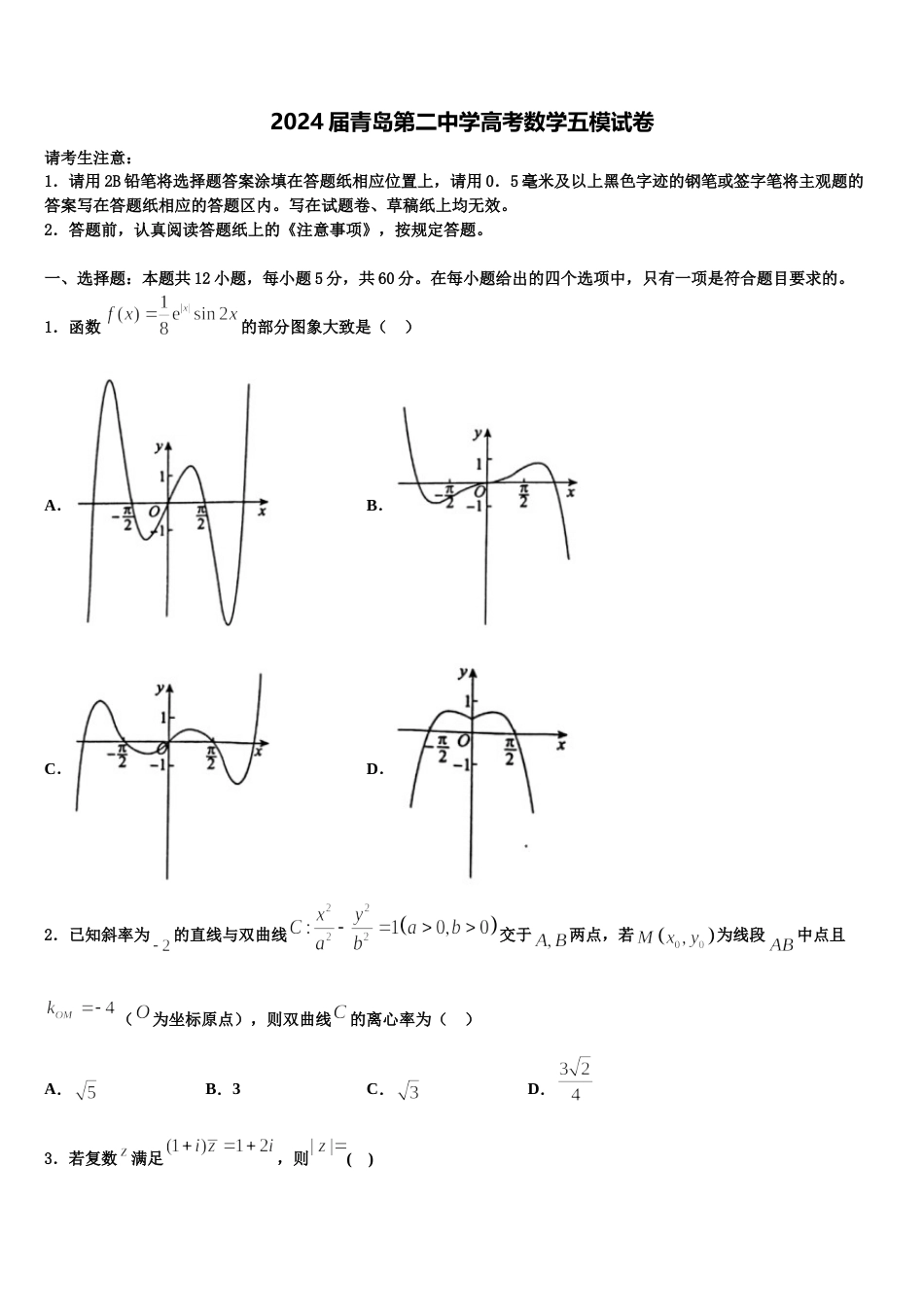
2024 届青岛第二中学高考数学五模试卷请考生注意:1.请用 2B 铅笔将选择题答案涂填在答题纸相应位置上,请用 0.5 毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.函数的部分图象大致是( )A.B.C.D.2.已知斜率为的直线与双曲线交于两点,若为线段中点且(为坐标原点),则双曲线的离心率为( )A.B.3C.D.3.若复数满足,则( )A.B.C.D.4.抛物线的焦点为,则经过点与点且与抛物线的准线相切的圆的个数有( )A.1 个B.2 个C.0 个D.无数个5.设集合 A={y|y=2x1﹣ ,x∈R},B={x|﹣2≤x≤3,x∈Z},则 A∩B=( )A.(﹣1,3]B.[1﹣ ,3]C.{0,1,2,3}D.{1﹣ ,0,1,2,3}6.已知函数 f(x)=eb﹣x﹣ex﹣b+c(b,c 均为常数)的图象关于点(2,1)对称,则 f(5)+f(﹣1)=( )A.﹣2B.﹣1C.2D.47.已知集合,,则等于( )A.B.C.D.8.如图,设为内一点,且,则与的面积之比为A.B.C.D.9.如图,在三棱锥中,平面,,现从该三棱锥的个表面中任选个,则选取的个表面互相垂直的概率为( )A.B.C.D.10.下列选项中,说法正确的是( )A.“”的否定是“”B.若向量满足 ,则与的夹角为钝角C.若,则D.“”是“”的必要条件11.为了进一步提升驾驶人交通安全文明意识,驾考新规要求驾校学员必须到街道路口执勤站岗,协助交警劝导交通.现有甲、乙等 5 名驾校学员按要求分配到三个不同的路口站岗,每个路口至少一人,且甲、乙在同一路口的分配方案共有( )A.12 种B.24 种C.36 种D.48 种12.已知向量,,则向量与的夹角为( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.将含有甲、乙、丙的 6 人平均分成两组参加“文明交通”志愿者活动,其中一组指挥交通,一组分发宣传资料,则甲、乙至少一人参加指挥交通且甲、丙不在同一个组的概率为__________.14.设实数 x,y 满足,则点表示的区域面积为______.15.已知函数()在区间上的值小于 0 恒成立,则的取值范围是________.16.已知函数在定义域 R 上的导函数为,若函数没有零点,且,当在上与在 R 上的单调性相同时,则实数 k 的取值范围是______.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)如图,平面四边形为直角梯形,,,,将绕着翻折到.(1)为上一点,且,当平面时,求实数的值;(2)当平面与平面所成的锐二面角大小为时,求与平面所成角的正弦.18.(12 分)已知椭圆:(),与轴负半轴交于,离心率.(1)求椭圆的方程;(2)设直线 :与椭圆交于,两点,连接,并延长交直线于,两点,已知,求证:直线恒过定点,并求出定点坐标.19.(12 分)已知命题:,;命题:函数无零点.(1)若为假,求实数的取值范围;(2)若为假,为真,求实数的取值范围.20.(12 分)已知中,角,,的对边分别为,,,已 知向量,且.(1)求角的大小;(2)若的面积为,,求.21.(12 分)如图,设点为椭圆的右焦点,圆过且斜率为的直线 交圆于两点,交椭圆于点两点,已知当时,(1)求椭圆的方程.(2)当时,求的面积.22.(10 分)已知等差数列的前 n 项和为,等比数列的前 n 项和为,且,,.(1)求数列与的通项公式;(2)求数列的前 n 项和.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、C【解析】判断函数的性质,和特殊值的正负,以及值域,逐一排除选项.【详解】,函数是奇函数,排除,时,,时,,排除,当时,, 时,,排除,符合条件,故选 C.【点睛】本题考查了根据函数解析式判断函数图象,属于基础题型,一般根据选项判断函数的奇偶性,零点,特殊值的正负,以及单调性,极值点等排除选项.2、B【解析】设,代入双曲线方程相减可得...