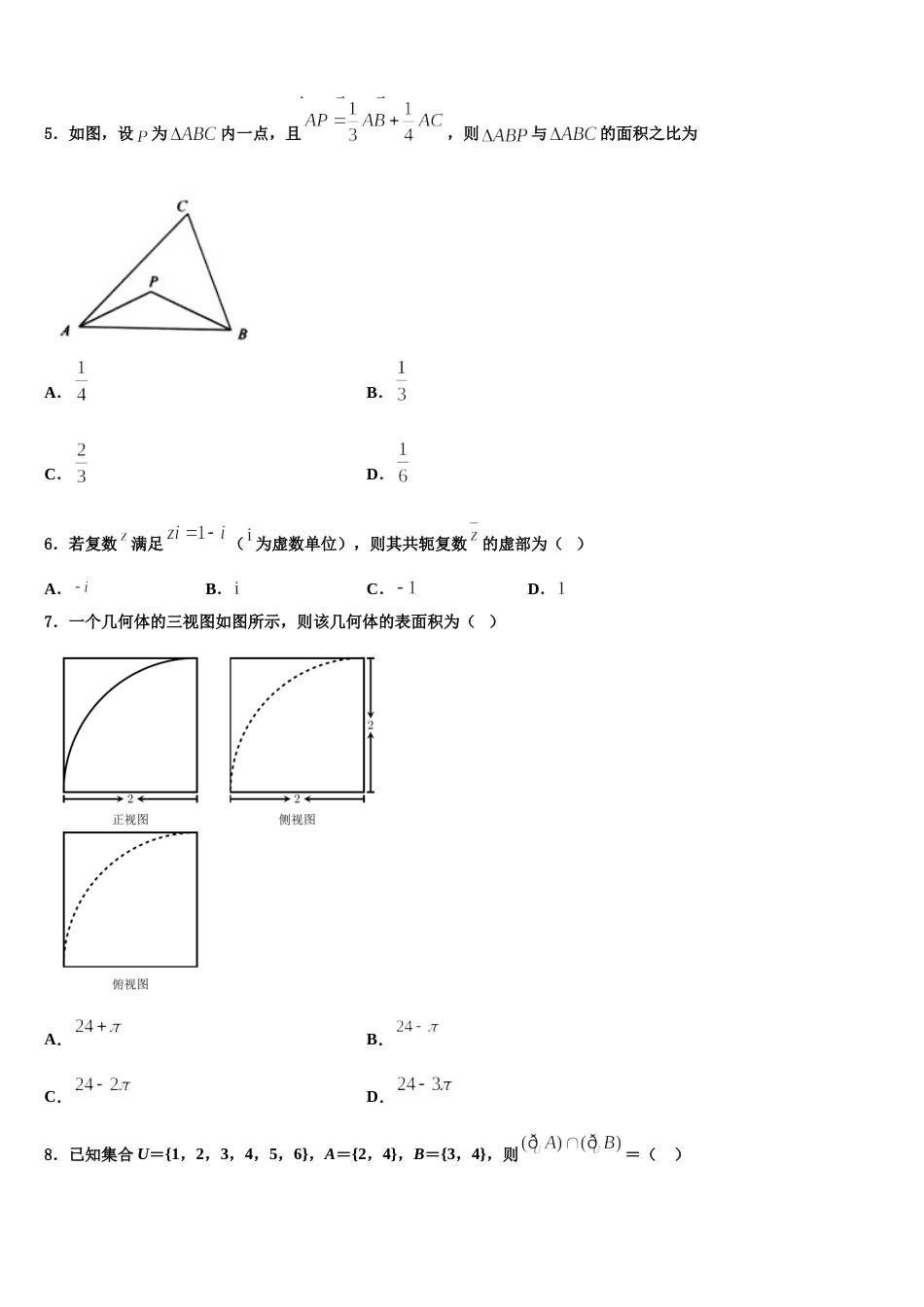
2024 届黑龙江省哈尔滨市呼兰区第一中学高考考前模拟数学试题考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用 2B 铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.如图,在平面四边形 ABCD 中,若点 E 为边 CD 上的动点,则的最小值为 ( )A.B.C.D.2.已知非零向量,满足,,则与的夹角为( )A.B.C.D.3.若 θ 是第二象限角且 sinθ =,则=A.B.C.D.4.若实数、满足,则的最小值是( )A.B.C.D.5.如图,设为内一点,且,则与的面积之比为A.B.C.D.6.若复数满足( 为虚数单位),则其共轭复数的虚部为( )A.B.C.D.7.一个几何体的三视图如图所示,则该几何体的表面积为( )A.B.C.D.8.已知集合 U={1,2,3,4,5,6},A={2,4},B={3,4},则=( )A.{3,5,6}B.{1,5,6}C.{2,3,4}D.{1,2,3,5,6}9.已知函数,若恒成立,则满足条件的的个数为( )A.0B.1C.2D.310.《九章算术》勾股章有一“引葭赴岸”问题“今有饼池径丈,葭生其中,出水两尺,引葭赴岸,适与岸齐,问水深,葭各几何?”,其意思是:有一个直径为一丈的圆柱形水池,池中心生有一颗类似芦苇的植物,露出水面两尺,若把它引向岸边,正好与岸边齐,问水有多深,该植物有多高?其中一丈等于十尺,如图若从该葭上随机取一点,则该点取自水下的概率为( )A.B.C.D.11.已知数列为等差数列,且,则的值为( )A.B.C.D.12.已知 为虚数单位,若复数,则A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.在一次体育水平测试中,甲、乙两校均有 100 名学生参加,其中:甲校男生成绩的优秀率为 70%,女生成绩的优秀率为 50%;乙校男生成绩的优秀率为 60%,女生成绩的优秀率为 40%.对于此次测试,给出下列三个结论:① 甲校学生成绩的优秀率大于乙校学生成绩的优秀率;② 甲、乙两校所有男生成绩的优秀率大于甲、乙两校所有女生成绩的优秀率;③ 甲校学生成绩的优秀率与甲、乙两校所有学生成绩的优秀率的大小关系不确定.其中,所有正确结论的序号是____________.14.在某批次的某种灯泡中,随机抽取 200 个样品.并对其寿命进行追踪调查,将结果列成频率分布表如下:寿命(天)频数频率40600.30.4200.1合计2001某人从灯泡样品中随机地购买了个,如果这个灯泡的寿命情况恰好与按四个组分层抽样所得的结果相同,则的最小值为______.15.若,则=____, = ___.16.(5 分)已知椭圆方程为,过其下焦点作斜率存在的直线 与椭圆交于两点,为坐标原点,则面积的取值范围是____________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知函数,.(1)求的值;(2)令在上最小值为,证明:.18.(12 分)△ABC 的内角的对边分别为,已知△ABC 的面积为(1)求;(2)若求△ABC 的周长.19.(12 分)a,b,c 分别为△ABC 内角 A,B,C 的对边.已知 a=3,,且 B=60°.(1)求△ABC 的面积; (2)若 D,E 是 BC 边上的三等分点,求.20.(12 分)如图,在正四棱柱中,,,过顶点,的平面与棱,分别交于,两点(不在棱的端点处).(1)求证:四边形是平行四边形;(2)求证:与不垂直;(3)若平面与棱所在直线交于点,当四边形为菱形时,求长.21.(12 分)已知函数,函数在点处的切线斜率为 0.(1)试用含有的式子表示,并讨论的单调性;(2)对于函数图象上的不同两点,,如果在函数图象上存在点,使得在点处的切线,则称存在“跟随切线”.特别地,当时,又称存在“中值跟随切线”.试问:函数上是否存在两点使得它存在“中值跟随切线”,若存在,求出的坐标,若不存在,说明理由.22.(10 分)已知数列为公差不为零的等差数列...