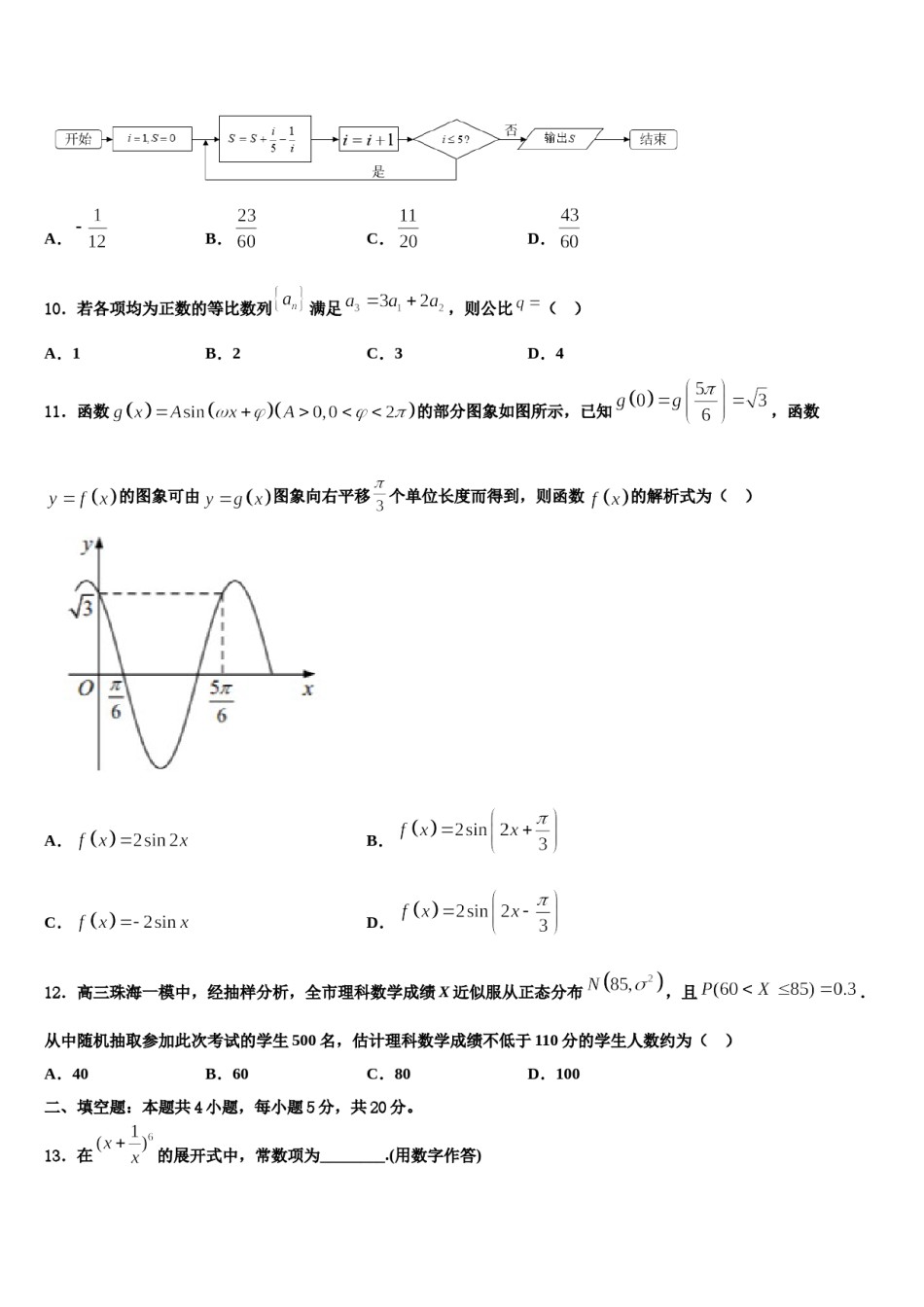
上海市上外附属大境中学2023-2024学年高考仿真模拟数学试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.函数满足对任意都有成立,且函数的图象关于点对称,,则B.2的值为()D.1A.0C.42.已知函数,满足对任意的实数,都有成立,则实数的取值范围为()A.B.C.D.3.《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中华文化,阴阳术数之源,其中河图的排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中.如图,白圈为阳数,黑点为阴数.若从这10个数中任取3个数,则这3个数中至少有2个阳数且能构成等差数列的概率为()A.B.C.D.4.若的展开式中的系数为-45,则实数的值为()A.B.2C.D.5.已知椭圆(a>b>0)与双曲线(a>0,b>0)的焦点相同,则双曲线渐近线方程为()A.B.C.D.6.已知向量,满足,在上投影为,则的最小值为()A.B.C.D.7.已知正方体的棱长为,,,分别是棱,,的中点,给出下列四个命题:①;②直线与直线所成角为;③过,,三点的平面截该正方体所得的截面为六边形;④三棱锥的体积为.其中,正确命题的个数为()A.B.C.D.8.已知等差数列{an},则“a2>a1”是“数列{an}为单调递增数列”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件9.执行下面的程序框图,则输出的值为()A.B.C.D.10.若各项均为正数的等比数列满足,则公比()C.3D.4A.1B.211.函数的部分图象如图所示,已知,函数的图象可由图象向右平移个单位长度而得到,则函数的解析式为()A.B.C.D.12.高三珠海一模中,经抽样分析,全市理科数学成绩X近似服从正态分布,且.从中随机抽取参加此次考试的学生500名,估计理科数学成绩不低于110分的学生人数约为()A.40B.60C.80D.100二、填空题:本题共4小题,每小题5分,共20分。13.在的展开式中,常数项为________.(用数字作答)14.已知,,是平面向量,是单位向量.若,,且,则的取值范围是________.15.如图,是圆的直径,弦的延长线相交于点垂直的延长线于点.求证:16.已知,复数且(为虚数单位),则__________,_________.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)如图,在四面体中,.(1)求证:平面平面;(2)若,二面角为,求异面直线与所成角的余弦值.18.(12分)已知函数.(1)求证:当时,;(2)若对任意存在和使成立,求实数的最小值.19.(12分)在中,内角的对边分别是,满足条件.(1)求角;(2)若边上的高为,求的长.20.(12分)已知椭圆:过点,过坐标原点作两条互相垂直的射线与椭圆分别交于,两点.(1)证明:当取得最小值时,椭圆的离心率为.(2)若椭圆的焦距为2,是否存在定圆与直线总相切?若存在,求定圆的方程;若不存在,请说明理由.21.(12分)设函数.(1)若,时,在上单调递减,求的取值范围;(2)若,,,求证:当时,.22.(10分)如图,已知平面与直线均垂直于所在平面,且.(1)求证:平面;所成角的正弦值.(2)若,求与平面参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、C【解析】根据函数的图象关于点对称可得为奇函数,结合可得是周期为4的周期函数,利用及可得所求的值.的图象关于原点对称,【详解】的图象关于点对称,所以因为函数所以为上的奇函数.由可得,故,故是周期为4的周期函数.因为,所以.因为,故,所以.故选:C.【点睛】本题考查函数的奇偶性和周期性,一般地,如果上的函数满足,那么是周期为的周期函数,本题属于中档题.2、B为上为减函数,可知函数为减函数,且,由此可解得【解析】由题意可知函数实...