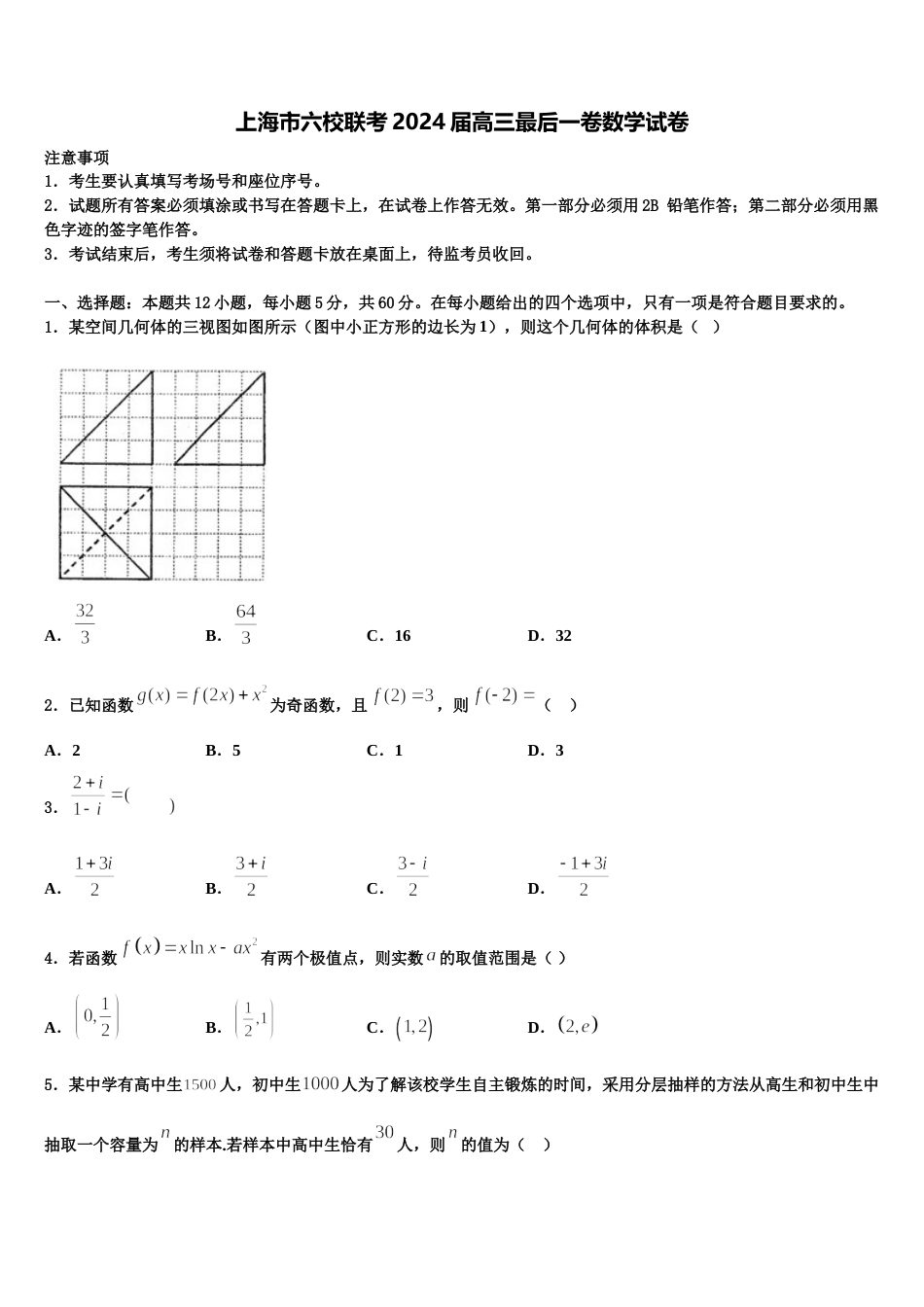
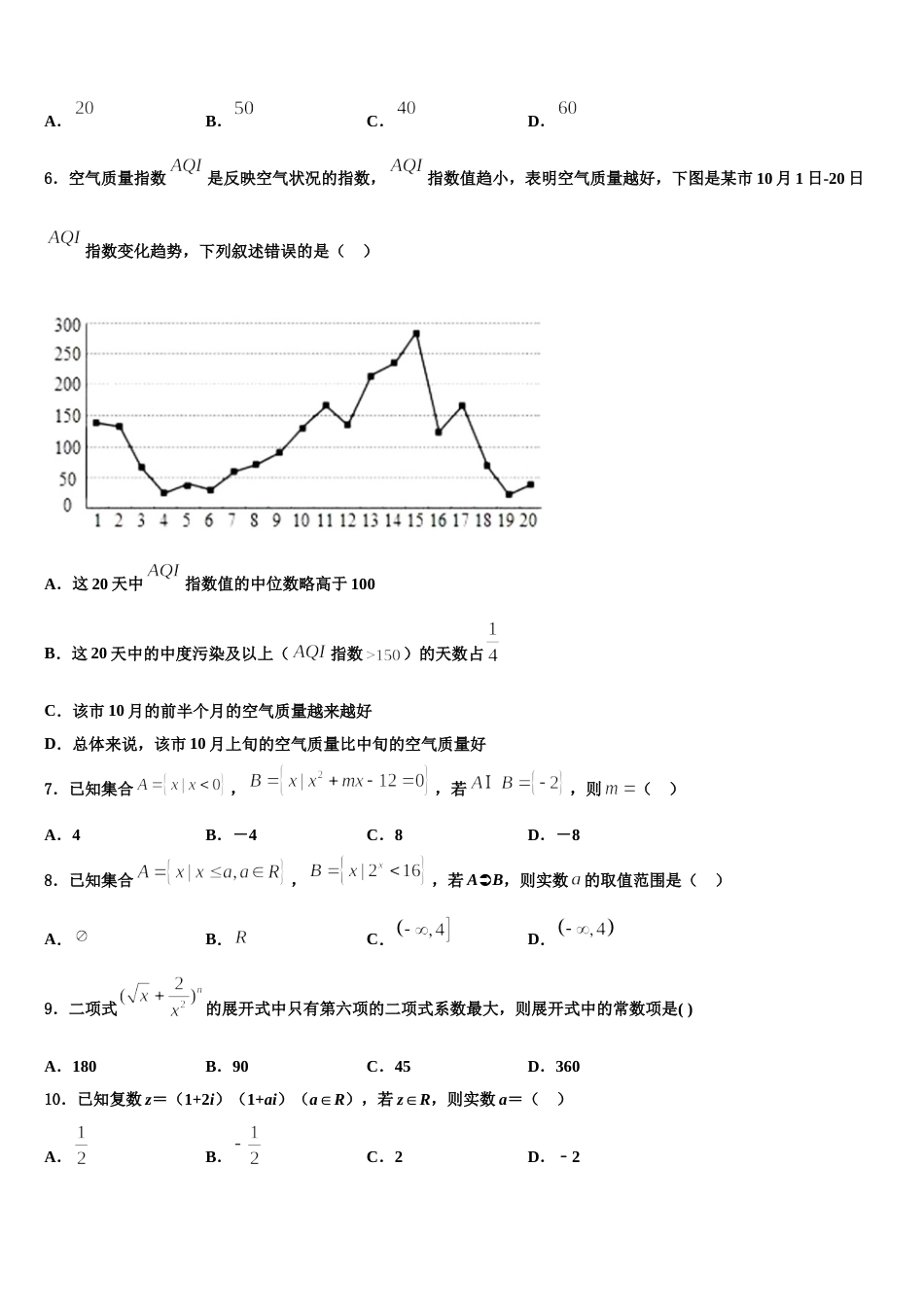
上海市六校联考 2024 届高三最后一卷数学试卷注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用 2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.某空间几何体的三视图如图所示(图中小正方形的边长为 1),则这个几何体的体积是( )A.B.C.16D.322.已知函数为奇函数,且,则( )A.2B.5C.1D.33. A.B.C.D.4.若函数有两个极值点,则实数的取值范围是( )A.B.C.D.5.某中学有高中生人,初中生人为了解该校学生自主锻炼的时间,采用分层抽样的方法从高生和初中生中抽取一个容量为的样本.若样本中高中生恰有人,则的值为( )A.B.C.D.6.空气质量指数是反映空气状况的指数,指数值趋小,表明空气质量越好,下图是某市 10 月 1 日-20 日指数变化趋势,下列叙述错误的是( )A.这 20 天中指数值的中位数略高于 100B.这 20 天中的中度污染及以上(指数)的天数占C.该市 10 月的前半个月的空气质量越来越好D.总体来说,该市 10 月上旬的空气质量比中旬的空气质量好7.已知集合,,若,则( )A.4B.-4C.8D.-88.已知集合,,若 AB,则实数的取值范围是( )A.B.C.D.9.二项式的展开式中只有第六项的二项式系数最大,则展开式中的常数项是( )A.180B.90C.45D.36010.已知复数 z=(1+2i)(1+ai)(a∈R),若 z∈R,则实数 a=( )A.B.C.2D.﹣211.一个几何体的三视图如图所示,则该几何体的表面积为( )A.B.C.D.12.在中,角、 、 的对边分别为、 、 ,若,,,则( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.在△ABC 中,∠BAC=,AD 为∠BAC 的角平分线,且,若 AB=2,则 BC=_______.14.已知三棱锥的四个顶点都在球的球面上,,则球的表面积为__________.15.过圆的圆心且与直线垂直的直线方程为__________.16.某种产品的质量指标值服从正态分布,且.某用户购买了件这种产品,则这件产品中质量指标值位于区间之外的产品件数为_________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知函数,其中.(Ⅰ)若,求函数的单调区间;(Ⅱ)设.若在上恒成立,求实数的最大值.18.(12 分)设函数.(Ⅰ)讨论函数的单调性;(Ⅱ)若函数有两个极值点,求证:.19.(12 分)已知椭圆的左右焦点分别是,点在椭圆上,满足(1)求椭圆的标准方程;(2)直线过点,且与椭圆只有一个公共点,直线与的倾斜角互补,且与椭圆交于异于点的两点,与直线交于点(介于两点之间),是否存在直线,使得直线,,的斜率按某种排序能构成等比数列?若能,求出的方程,若不能,请说理由.20.(12 分)已知.(1)解关于 x 的不等式:;(2)若的最小值为 M,且,求证:.21.(12 分)已知的三个内角所对的边分别为,向量,,且.(1)求角的大小;(2)若,求的值22.(10 分)某工厂为提高生产效率,需引进一条新的生产线投入生产,现有两条生产线可供选择,生产线①:有A,B 两道独立运行的生产工序,且两道工序出现故障的概率依次是 0.02,0.03.若两道工序都没有出现故障,则生产成本为 15 万元;若 A 工序出现故障,则生产成本增加 2 万元;若 B 工序出现故障,则生产成本增加 3 万元;若 A,B两道工序都出现故障,则生产成本增加 5 万元.生产线②:有 a,b 两道独立运行的生产工序,且两道工序出现故障的概率依次是 0.04,0.01.若两道工序都没有出现故障,则生产成本为 14 万元;若 a 工序出现故障,则生产成本增加 8 万元;若 b 工序出现故障,则生产成本增加 5 万元;若 a,b 两道工序都出现故障,则生产成本增加 13 万元.(1)若选择生产线①,求生产成本恰好为 18 万元的概率;(2)为最大限度节约生产成本,你会...