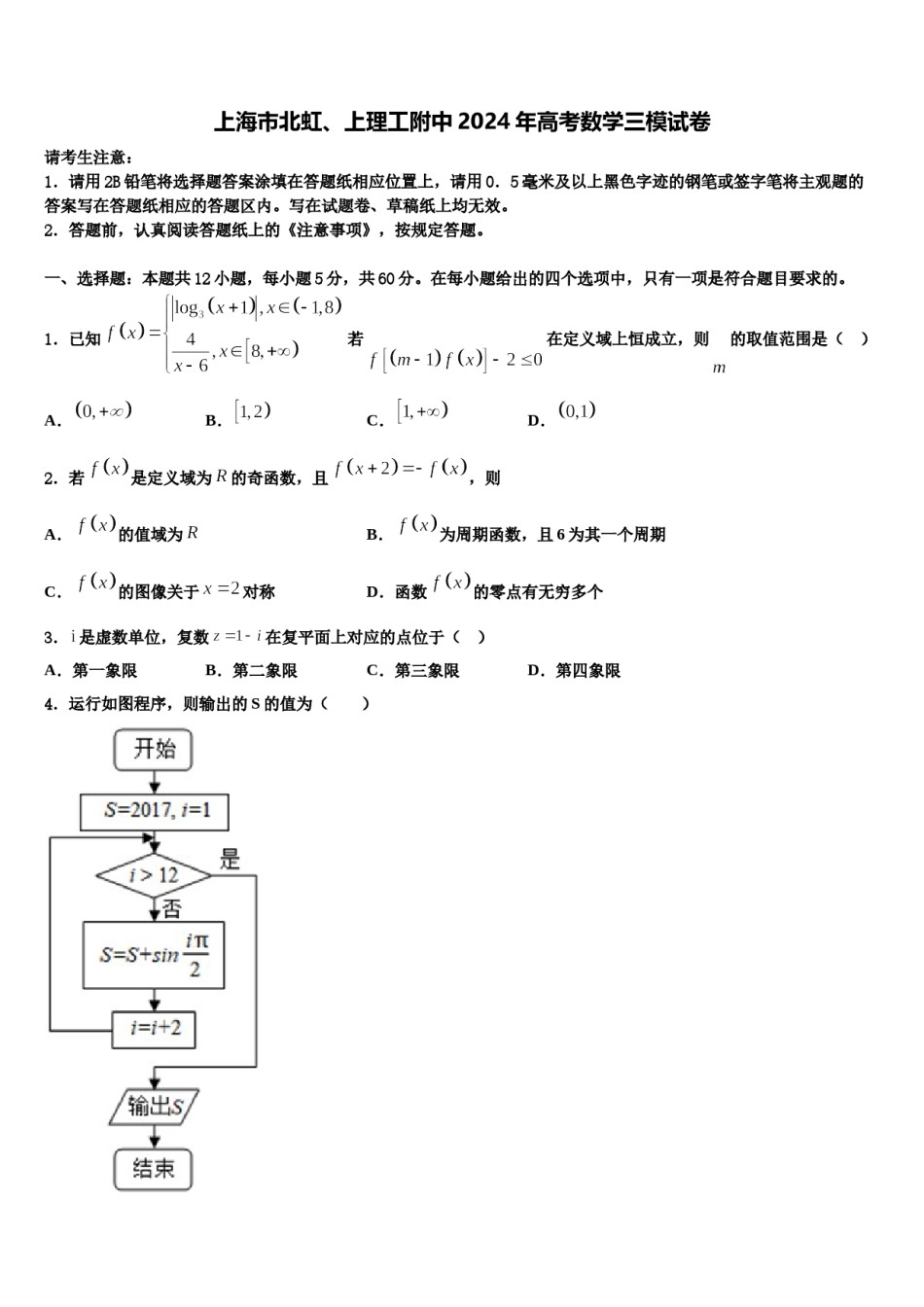
上海市北虹、上理工附中2024年高考数学三模试卷请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知若在定义域上恒成立,则的取值范围是()A.B.C.D.2.若是定义域为的奇函数,且,则A.的值域为B.为周期函数,且6为其一个周期C.的图像关于对称D.函数的零点有无穷多个3.是虚数单位,复数在复平面上对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限4.运行如图程序,则输出的S的值为()A.0B.1C.2018D.20175.已知,且,则的值为()A.B.C.D.6.已知三棱锥且平面,其外接球体积为()A.B.C.D.7.已知命题p:直线a∥b,且b⊂平面α,则a∥α;命题q:直线l⊥平面α,任意直线m⊂α,则l⊥m.下列命题为真命题的是()B.p∨(非q)C.(非p)∧qD.p∧(非q)A.p∧q8.若函数有且仅有一个零点,则实数的值为()A.B.C.D.9.某四棱锥的三视图如图所示,则该四棱锥的体积为()A.B.C.D.10.在中,角的对边分别为,,若,,且,则的面积为()A.B.C.D.11.某校8位学生的本次月考成绩恰好都比上一次的月考成绩高出50分,则以该8位学生这两次的月考成绩各自组成样本,则这两个样本不变的数字特征是()A.方差B.中位数C.众数D.平均数12.设,,,则、、的大小关系为()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.从编号为,,,的张卡片中随机抽取一张,放回后再随机抽取一张,则第二次抽得的卡片上的数字能被第一次抽得的卡片上数字整除的概率为_____________.14.已知半径为4的球面上有两点,,球心为O,若球面上的动点C满足二面角的大小为,则四面体的外接球的半径为_________.15.已知一组数据,1,0,,的方差为10,则________16.已知向量,,则______.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知,函数有最小值7.(1)求的值;(2)设,,求证:.18.(12分)数列满足,是与的等差中项.(1)证明:数列为等比数列,并求数列的通项公式;(2)求数列的前项和.19.(12分)设椭圆的左右焦点分别为,离心率是,动点在椭圆上运动,当轴时,.(1)求椭圆的方程;(2)延长分别交椭圆于点(不重合).设,求的最小值.20.(12分)在中,角的对边分别为.已知,.(1)若,求;(2)求的面积的最大值.21.(12分)如图,湖中有一个半径为千米的圆形小岛,岸边点与小岛圆心相距千米,为方便游人到小岛观光,从点向小岛建三段栈道,,,湖面上的点在线段上,且,均与圆相切,切点分别为,,其中栈道,,和小岛在同一个平面上.沿圆的优弧(圆上实线部分)上再修建栈道.记为.用表示栈道的总长度,并确定的取值范围;求当为何值时,栈道总长度最短.22.(10分)已知椭圆的离心率为,直线过椭圆的右焦点,过的直线交椭圆于两点(均异于左、右顶点).(1)求椭圆的方程;(2)已知直线,为椭圆的右顶点.若直线交于点,直线交于点,试判断是否为定值,若是,求出定值;若不是,说明理由.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、C【解析】先解不等式,可得出,求出函数的值域,由题意可知,不等式在定义域上恒成立,可得出关于的不等式,即可解得实数的取值范围.【详解】,先解不等式.①当时,由,得,解得,此时;②当时,由,得.所以,不等式的解集为.下面来求函数的值域.,此时,则.当时,,;当时,,此时综上所述,函数的值域为由于在定义域上恒成立,则不等式在定义域上恒成立,所以,,解得.因此,实数的取值范围是.故选:C.【点睛】本题考查利用函数不等式恒成立求参数,同时也考查了分段函数基本性质的应用,考查分类讨论思想的应用,属于中等题.2、D【解析】运用函数的奇偶性定义,周期性定义,根据表达式判断...