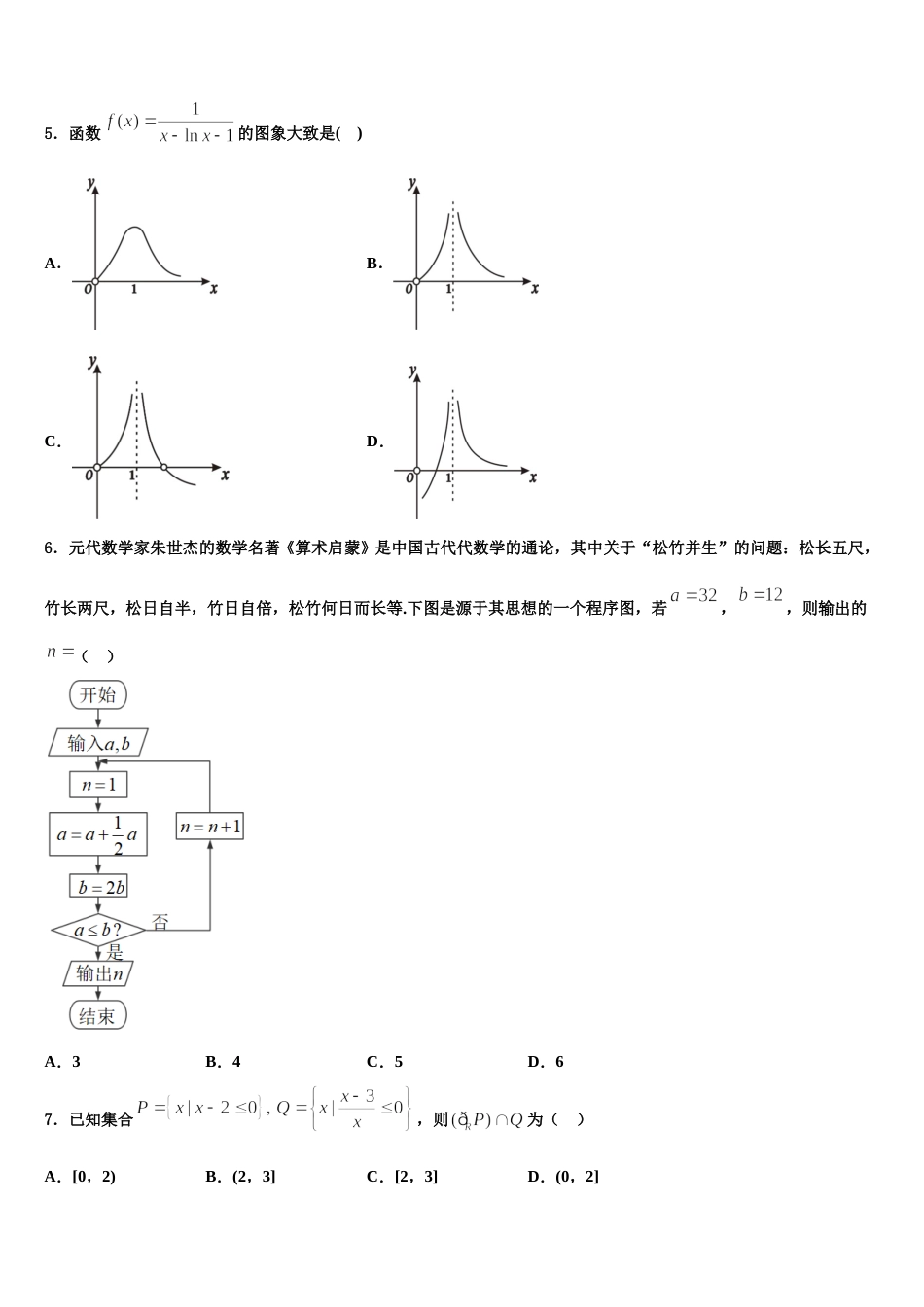
上海市嘉定一中 2024 年高考数学四模试卷请考生注意:1.请用 2B 铅笔将选择题答案涂填在答题纸相应位置上,请用 0.5 毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.若,则实数的大小关系为( )A.B.C.D.2.给出以下四个命题:① 依次首尾相接的四条线段必共面;② 过不在同一条直线上的三点,有且只有一个平面;③ 空间中如果一个角的两边与另一个角的两边分别平行,那么这两个角必相等;④ 垂直于同一直线的两条直线必平行.其中正确命题的个数是( )A.0B.1C.2D.33.下图是民航部门统计的某年春运期间,六个城市售出的往返机票的平均价格(单位元),以及相比于上一年同期价格变化幅度的数据统计图,以下叙述不正确的是( )A.深圳的变化幅度最小,北京的平均价格最高B.天津的往返机票平均价格变化最大C.上海和广州的往返机票平均价格基本相当D.相比于上一年同期,其中四个城市的往返机票平均价格在增加4.已知数列满足,则( )A.B.C.D.5.函数的图象大致是( )A.B.C.D.6.元代数学家朱世杰的数学名著《算术启蒙》是中国古代代数学的通论,其中关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.下图是源于其思想的一个程序图,若,,则输出的( )A.3B.4C.5D.67.已知集合,则为( )A.[0,2)B.(2,3]C.[2,3]D.(0,2]8.下列说法正确的是( )A.“若,则”的否命题是“若,则”B.“若,则”的逆命题为真命题C.,使成立D.“若,则”是真命题9.已知数列满足,且成等比数列.若的前 n 项和为,则的最小值为( )A.B.C.D.10.集合的真子集的个数是( )A.B.C.D.11.为了加强“精准扶贫”,实现伟大复兴的“中国梦”,某大学派遣甲、乙、丙、丁、戊五位同学参加三个贫困县的调研工作,每个县至少去 1 人,且甲、乙两人约定去同一个贫困县,则不同的派遣方案共有( )A.24B.36C.48D.6412.已知 为虚数单位,若复数,则A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.正方体的棱长为 2, 是它的内切球的一条弦(我们把球面上任意两点之间的线段称为球的弦), 为正方体表面上的动点,当弦的长度最大时, 的取值范围是______.14.已知是定义在上的奇函数,当时,,则不等式的解集用区间表示为__________.15.在长方体中,,,,为的中点,则点到平面的距离是______.16.已知圆,直线 与圆交于两点,,若,则弦的长度的最大值为_______.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知等差数列和等比数列满足:(I)求数列和的通项公式;(II)求数列的前 项和.18.(12 分)(江苏省徐州市高三第一次质量检测数学试题)在平面直角坐标系中,已知平行于轴的动直线交抛物线: 于点,点为的焦点.圆心不在轴上的圆与直线 , , 轴都相切,设的轨迹为曲线.(1)求曲线的方程;(2)若直线与曲线相切于点,过且垂直于的直线为,直线, 分别与轴相交于点, .当线段的长度最小时,求 的值.19.(12 分)已知函数.(1)讨论的零点个数;(2)证明:当时,.20.(12 分)如图,三棱柱中,底面是等边三角形,侧面是矩形,是的中点,是棱上的点,且.(1)证明:平面;(2)若,求二面角的余弦值.21.(12 分)如图,在四棱锥中,平面,,为的中点.(1)求证:平面;(2)求二面角的余弦值.22.(10 分)己知的内角的对边分别为.设(1)求的值;(2)若,且,求的值.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、A【解析】将化成以 为底的对数,即可判断 的大小关系;由对数函数、指数函数的性质,可判断出 与 1 的大小关系,从而可判断三者的大小关系.【详解】依题意,由对数函数的性质可...