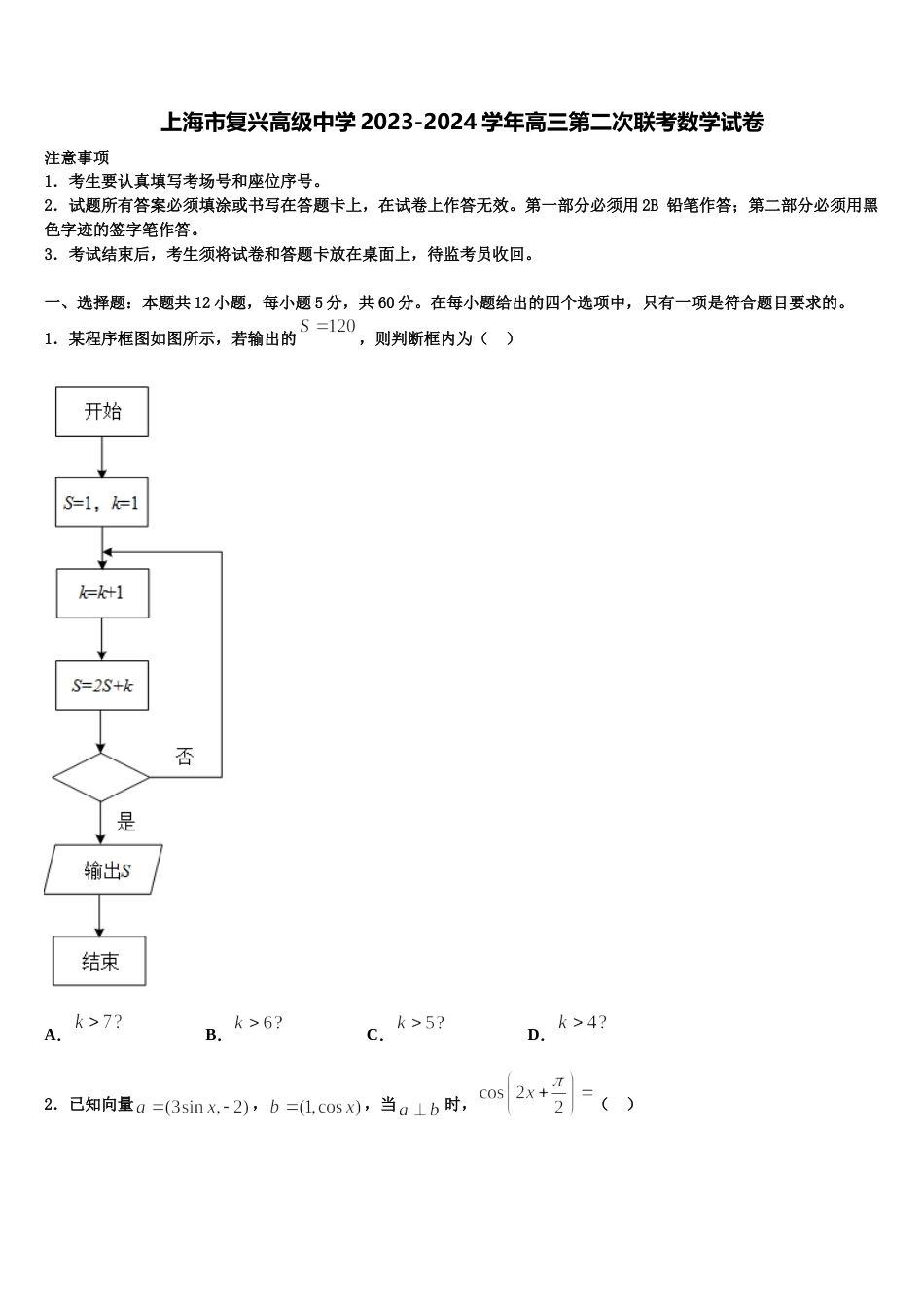
上海市复兴高级中学 2023-2024 学年高三第二次联考数学试卷注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用 2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.某程序框图如图所示,若输出的,则判断框内为( )A.B.C.D.2.已知向量,,当时,( )A.B.C.D.3.将 4 名大学生分配到 3 个乡镇去当村官,每个乡镇至少一名,则不同的分配方案种数是( )A.18 种B.36 种C.54 种D.72 种4.如图,在中,,是上一点,若,则实数 的值为( )A.B.C.D.5.已知奇函数是上的减函数,若满足不等式组,则的最小值为( )A.-4B.-2C.0D.46.已知函数,关于 x 的方程 f(x)=a 存在四个不同实数根,则实数 a 的取值范围是( )A.(0,1)∪(1,e)B.C.D.(0,1)7.如果实数满足条件,那么的最大值为( )A.B.C.D.8.在展开式中的常数项为 A.1B.2C.3D.79.一袋中装有个红球和个黑球(除颜色外无区别),任取球,记其中黑球数为,则为( )A.B.C.D.10.已知是等差数列的前项和,,,则( )A.85B.C.35D.11.已知条件,条件直线与直线平行,则是的( )A.充要条件B.必要不充分条件C.充分不必要条件D.既不充分也不必要条件12.已知函数 f(x)=sin2x+sin2(x),则 f(x)的最小值为( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知实数,且由的最大值是_________14.已知正方形边长为,空间中的动点满足,,则三棱锥体积的最大值是______.15.已知数列满足:点在直线上,若使、、构成等比数列,则______16.边长为 2 的正方形经裁剪后留下如图所示的实线围成的部分,将所留部分折成一个正四棱锥.当该棱锥的体积取得最大值时,其底面棱长为________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知数列,其前项和为,若对于任意,,且,都有.(1)求证:数列是等差数列(2)若数列满足,且等差数列的公差为,存在正整数,使得,求的最小值.18.(12 分)如图所示,在三棱锥中,,,,点为中点.(1)求证:平面平面;(2)若点为中点,求平面与平面所成锐二面角的余弦值.19.(12 分)已知函数.(1)解关于的不等式;(2)若函数的图象恒在直线的上方,求实数的取值范围20.(12 分)如图,底面是等腰梯形,,点为的中点,以为边作正方形,且平面平面.(1)证明:平面平面.(2)求二面角的正弦值.21.(12 分)已知函数.(1)当时.① 求函数在处的切线方程;② 定义其中,求;(2)当时,设,( 为自然对数的底数),若对任意给定的,在上总存在两个不同的,使得成立,求的取值范围.22.(10 分)已知奇函数的定义域为,且当时,.(1)求函数的解析式;(2)记函数,若函数有 3 个零点,求实数的取值范围.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、C【解析】程序在运行过程中各变量值变化如下表: K S 是否继续循环循环前11 第一圈24是第二圈311是第三圈 426是第四圈 557是第五圈 6120否故退出循环的条件应为 k>5?本题选择 C 选项.点睛:使用循环结构寻数时,要明确数字的结构特征,决定循环的终止条件与数的结构特征的关系及循环次数.尤其是统计数时,注意要统计的数的出现次数与循环次数的区别.2、A【解析】根据向量的坐标运算,求出,,即可求解.【详解】,.故选:A.【点睛】本题考查向量的坐标运算、诱导公式、二倍角公式、同角间的三角函数关系,属于中档题.3、B【解析】把 4 名大学生按人数分成 3 组,为 1 人、1 人、2 人,再把这三组分配到 3 个乡镇即得.【详解】把 4 名大学生按人数分成 3 组,为 1 人、1 人、2 人,再把这三组分配到 3 ...