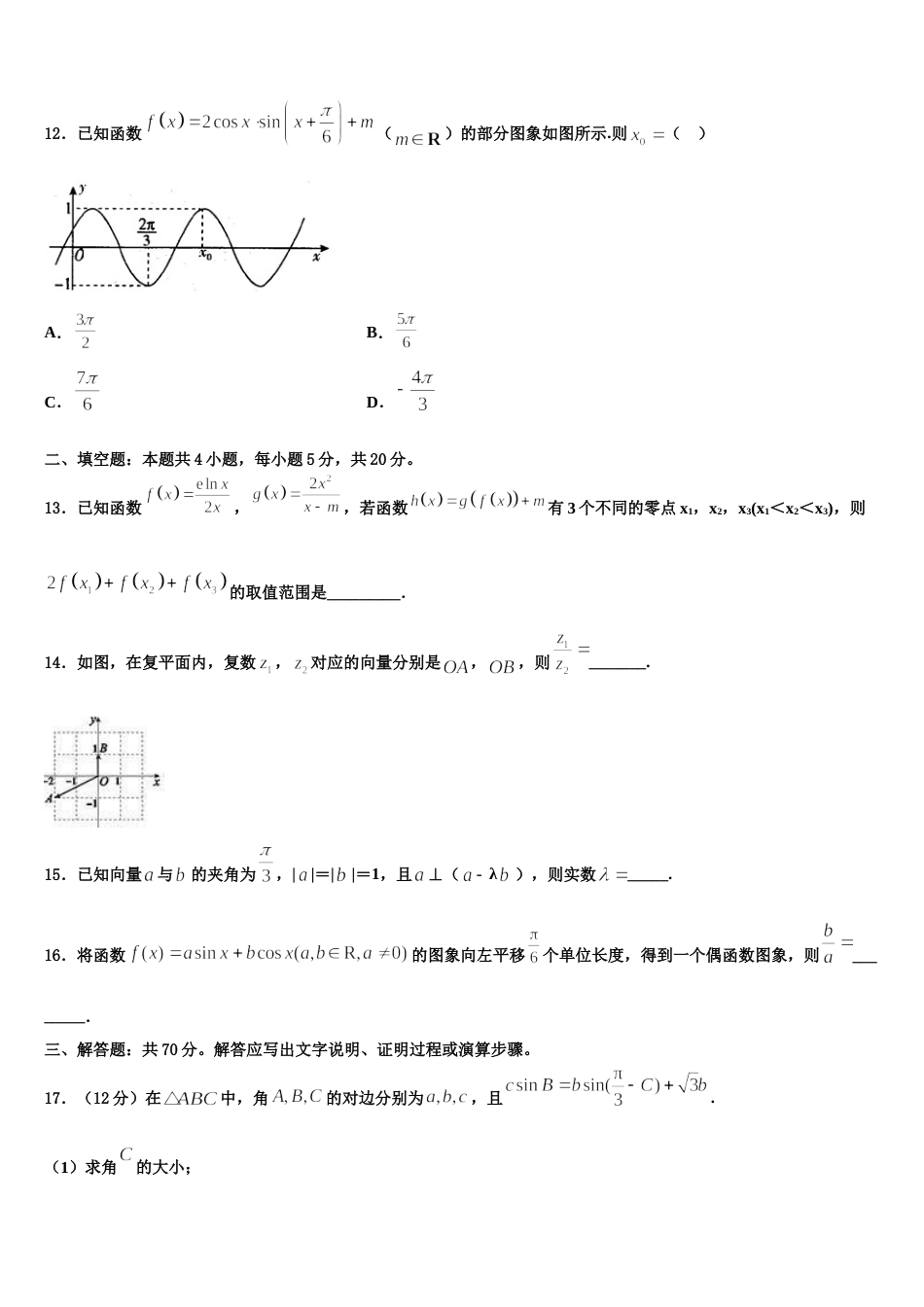
上海市建平中学 2024 届高三 3 月份模拟考试数学试题注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知集合,,,则( )A.B.C.D.2.若变量,满足,则的最大值为( )A.3B.2C.D.103. 的内角的对边分别为,已知,则角的大小为( )A.B.C.D.4.若复数满足( 是虚数单位),则的虚部为( )A.B.C.D.5.已知点 P 不在直线 l、m 上,则“过点 P 可以作无数个平面,使得直线 l、m 都与这些平面平行”是“直线 l、m 互相平行”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件6.设某大学的女生体重 y(单位:kg)与身高 x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为=0.85x-85.71,则下列结论中不正确的是A.y 与 x 具有正的线性相关关系B.回归直线过样本点的中心(,)C.若该大学某女生身高增加 1cm,则其体重约增加 0.85kgD.若该大学某女生身高为 170cm,则可断定其体重比为 58.79kg7.已知正四棱锥的侧棱长与底面边长都相等,是的中点,则所成的角的余弦值为( )A.B.C.D.8.定义两种运算“★”与“◆”,对任意,满足下列运算性质:①★,◆;②()★★ ,◆◆,则(◆2020)(2020★2018)的值为( )A.B.C.D.9.在三棱锥中,,且分别是棱,的中点,下面四个结论:①;②平面;③ 三棱锥的体积的最大值为;④与一定不垂直.其中所有正确命题的序号是( )A.①②③B.②③④C.①④D.①②④10.复数满足为虚数单位),则的虚部为( )A.B.C.D.11.已知函数,若函数有三个零点,则实数的取值范围是( )A.B.C.D.12.已知函数()的部分图象如图所示.则( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知函数,,若函数有 3 个不同的零点 x1,x2,x3(x1<x2<x3),则的取值范围是_________.14.如图,在复平面内,复数,对应的向量分别是,,则_______.15.已知向量与的夹角为,||=||=1,且⊥(λ),则实数_____.16.将函数的图象向左平移个单位长度,得到一个偶函数图象,则________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)在中,角的对边分别为,且.(1)求角的大小;(2)若,求边上的高.18.(12 分)设点,分别是椭圆的左、右焦点,为椭圆上任意一点,且的最小值为 1.(1)求椭圆的方程;(2)如图,动直线与椭圆有且仅有一个公共点,点,是直线 上的两点,且,,求四边形面积的最大值.19.(12 分)在某外国语学校举行的(高中生数学建模大赛)中,参与大赛的女生与男生人数之比为,且成绩分布在,分数在以上(含)的同学获奖.按女生、男生用分层抽样的方法抽取人的成绩作为样本,得到成绩的频率分布直方图如图所示.( )Ⅰ 求的值,并计算所抽取样本的平均值(同一组中的数据用该组区间的中点值作代表);()Ⅱ 填写下面的列联表,并判断在犯错误的概率不超过的前提下能否认为“获奖与女生、男生有关”.女生男生总计获奖不获奖总计附表及公式:其中,.20.(12 分)如图,为坐标原点,点为抛物线的焦点,且抛物线上点处的切线与圆相切于点(1)当直线的方程为时,求抛物线的方程;(2)当正数变化时,记分别为的面积,求的最小值.21.(12 分)有甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司底薪元,送餐员每单制成元;乙公司无底薪,单以内(含单)的部分送餐员每单抽成元,超过单的部分送餐员每单抽成元.现从这两家公司各随机选取一名送餐员,分别记录其天的送餐单数,得到如下频数分布表:送餐单数3839404142甲公司天数1...