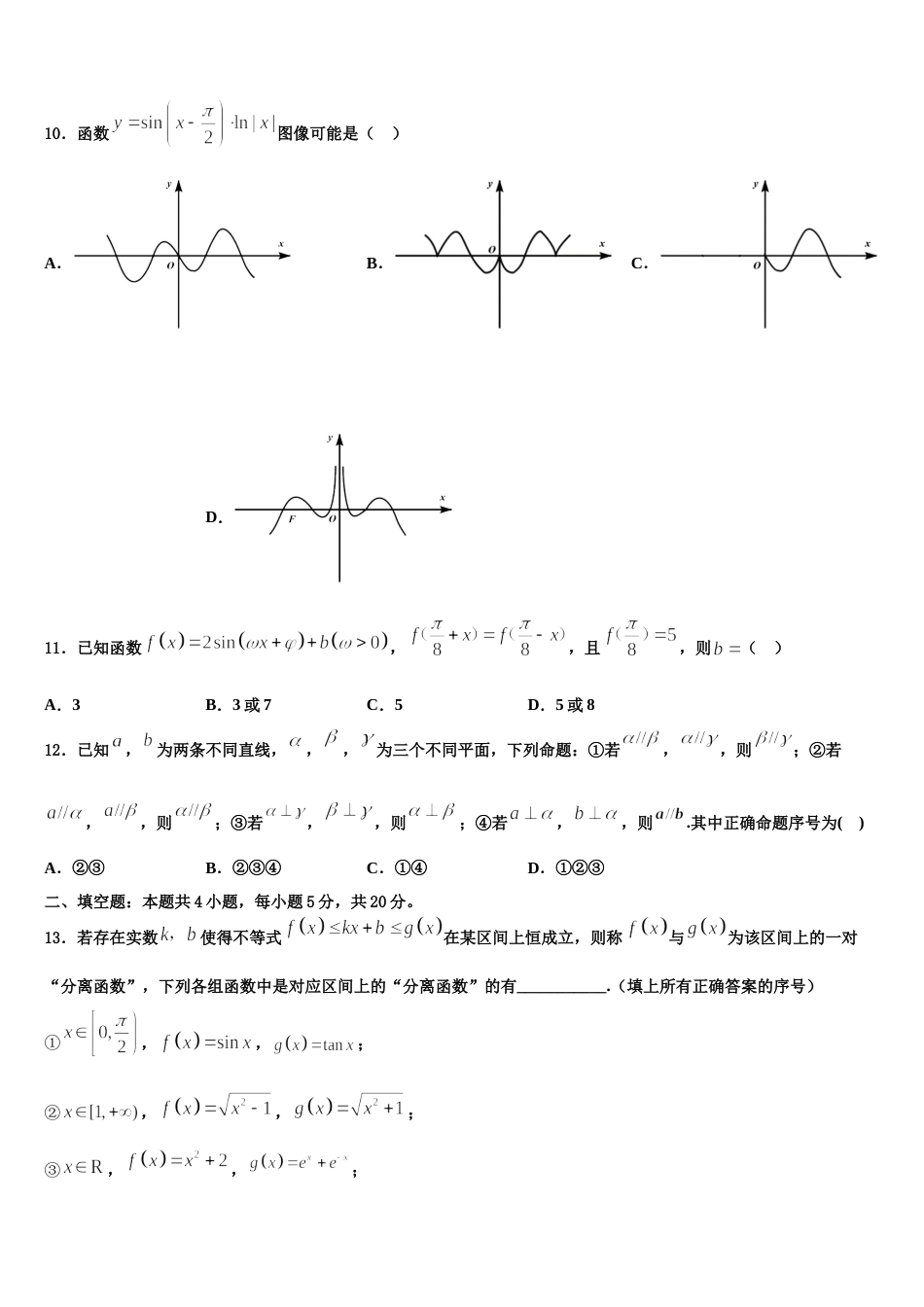
上海市鲁迅中学 2023-2024 学年高考数学五模试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.己知函数若函数的图象上关于原点对称的点有 2 对,则实数的取值范围是( )A.B.C.D.2.设,命题“存在,使方程有实根”的否定是( )A.任意,使方程无实根B.任意,使方程有实根C.存在,使方程无实根D.存在,使方程有实根3.已知集合,,则( )A.B.C.D.4.已知变量的几组取值如下表:12347若与线性相关,且,则实数( )A.B.C.D.5.过抛物线的焦点且与的对称轴垂直的直线 与交于,两点,,为的准线上的一点,则的面积为( )A.1B.2C.4D.86.公元 263 年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值,这就是著名的“徽率”。如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的值为( )(参考数据: )A.48B.36C.24D.127.已知直线 :与圆:交于,两点,与 平行的直线与圆交于,两点,且与的面积相等,给出下列直线:①,②,③,④.其中满足条件的所有直线的编号有( )A.①②B.①④C.②③D.①②④8.已知函数,则在上不单调的一个充分不必要条件可以是( )A.B.C.或D.9.已知数列为等差数列,为其前 项和,,则( )A.B.C.D.10.函数图像可能是( )A.B.C.D.11.已知函数,,且,则( )A.3B.3 或 7C.5D.5 或 812.已知,为两条不同直线,,,为三个不同平面,下列命题:①若,,则;②若,,则;③若,,则;④若,,则.其中正确命题序号为( )A.②③B.②③④C.①④D.①②③二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.若存在实数使得不等式在某区间上恒成立,则称与为该区间上的一对“分离函数”,下列各组函数中是对应区间上的“分离函数”的有___________.(填上所有正确答案的序号)①,,;②,,;③,,;④,,.14.若函数恒成立,则实数的取值范围是_____.15.在中,,是的角平分线,设,则实数的取值范围是__________.16.函数的定义域为,其图象如图所示.函数是定义域为的奇函数,满足,且当时,.给出下列三个结论: ①;② 函数在内有且仅有个零点;③ 不等式的解集为.其中,正确结论的序号是________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)如图,在四棱柱中,平面,底面 ABCD 满足∥BC,且( )Ⅰ 求证:平面;()Ⅱ 求直线与平面所成角的正弦值.18.(12 分)在直角坐标系中,圆的参数方程为:(为参数),以坐标原点为极点,以轴的正半轴为极轴建立极坐标系,且长度单位相同.(1)求圆的极坐标方程;(2)若直线 :( 为参数)被圆截得的弦长为,求直线 的倾斜角.19.(12 分)已知函数与的图象关于直线对称. ( 为自然对数的底数)(1)若的图象在点处的切线经过点,求的值;(2)若不等式恒成立,求正整数的最小值.20.(12 分)如图,在三棱柱中,,,,为的中点,且.(1)求证:平面;(2)求锐二面角的余弦值.21.(12 分)若数列满足:对于任意,均为数列中的项,则称数列为“数列”.(1)若数列的前项和,,试判断数列是否为“数列”?说明理由;(2)若公差为的等差数列为“数列”,求的取值范围;(3)若数列为“数列”,,且对于任意,均有,求数列的通项公式.22.(10 分)(1)求曲线和曲线围成图形的面积;(2)化简求值:.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、B【解析】考虑当时,...