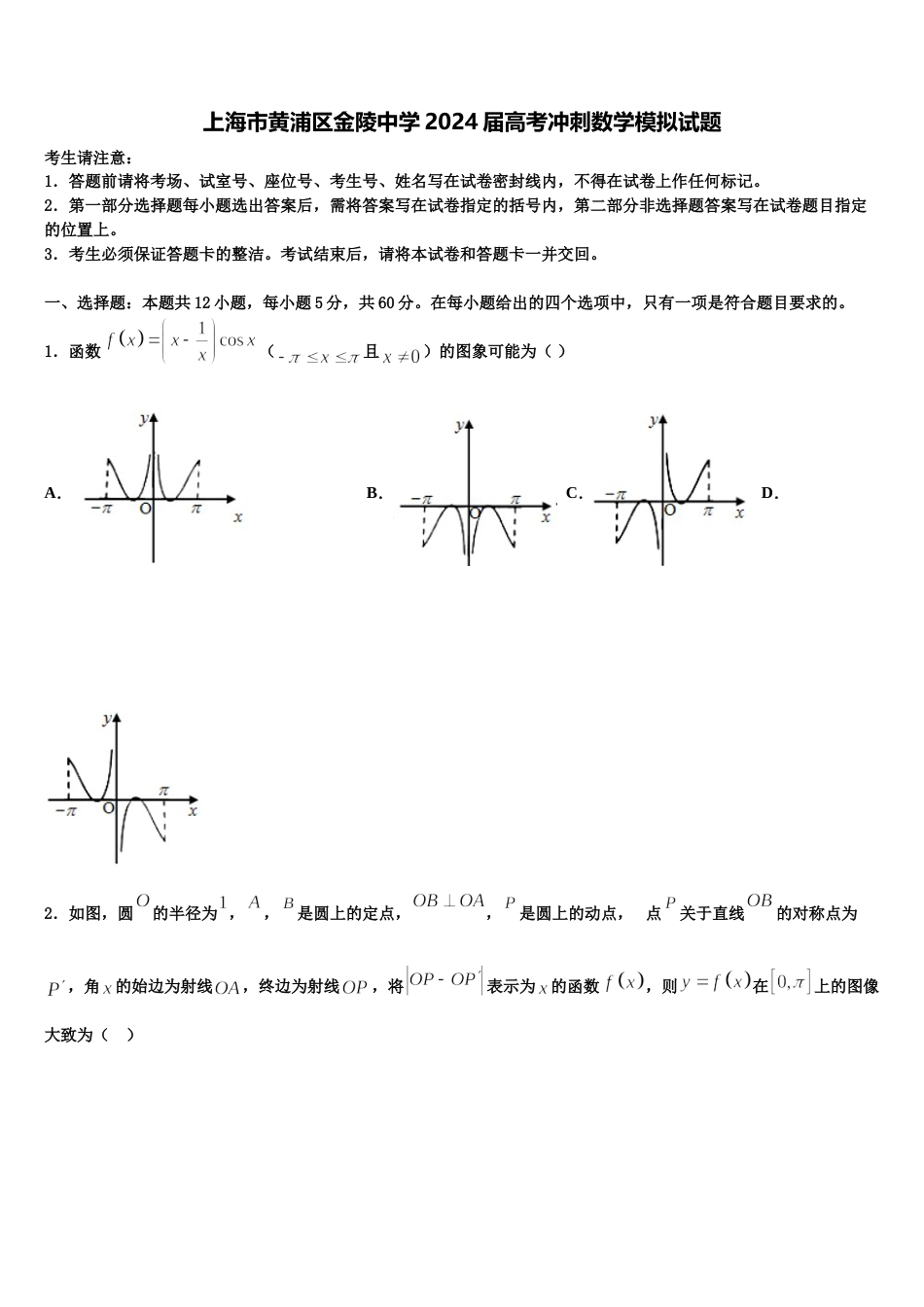
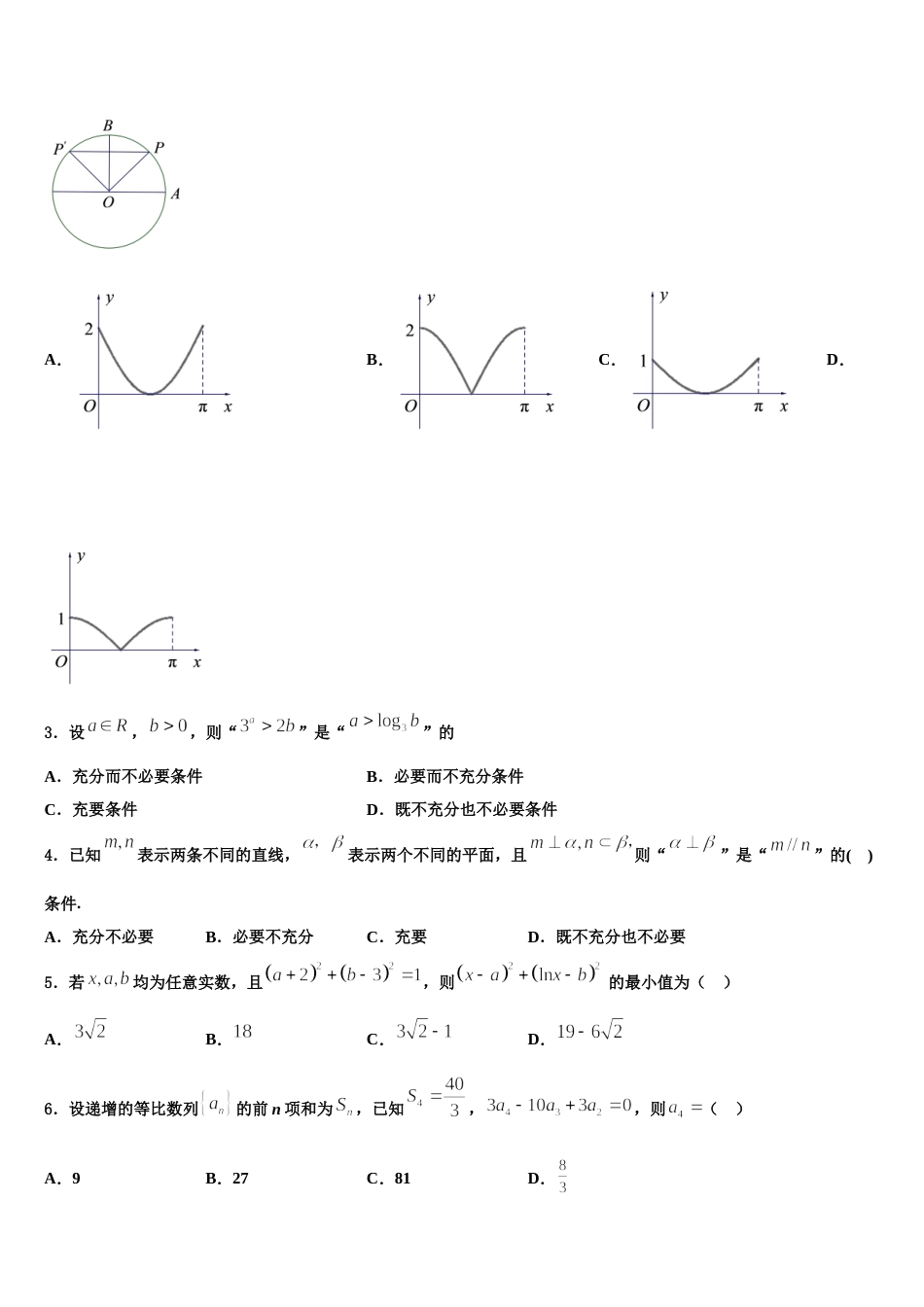
上海市黄浦区金陵中学 2024 届高考冲刺数学模拟试题考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.函数(且)的图象可能为( )A.B.C.D.2.如图,圆的半径为 ,,是圆上的定点,,是圆上的动点, 点关于直线的对称点为,角的始边为射线,终边为射线,将表示为的函数,则在上的图像大致为( )A.B.C.D.3.设,,则“”是“”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件4.已知表示两条不同的直线,表示两个不同的平面,且则“”是“”的( )条件.A.充分不必要B.必要不充分C.充要D.既不充分也不必要5.若均为任意实数,且,则 的最小值为( )A.B.C.D.6.设递增的等比数列的前 n 项和为,已知,,则( )A.9B.27C.81D.7.已知复数满足,则的共轭复数是( )A.B.C.D.8.若,则( )A.B.C.D.9.已知集合,集合,则( )A.B.C.D.10.已知双曲线的一条渐近线倾斜角为,则( )A.3B.C.D.11.已知角的顶点与坐标原点重合,始边与轴的非负半轴重合,它的终边过点,则的值为( )A.B.C.D.12.记其中表示不大于 x 的最大整数,若方程在在有 7 个不同的实数根,则实数 k 的取值范围( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.在各项均为正数的等比数列中,,且,成等差数列,则___________.14.六位同学坐在一排,现让六位同学重新坐,恰有两位同学坐自己原来的位置,则不同的坐法有________种(用数字回答).15.某校为了解家长对学校食堂的满意情况,分别从高一、高二年级随机抽取了 20 位家长的满意度评分,其频数分布表如下:满意度评分分组合计高一1366420高二2655220根据评分,将家长的满意度从低到高分为三个等级:满意度评分评分70 分70评分90评分90 分满意度等级不满意满意非常满意假设两个年级家长的评价结果相互独立,根据所给数据,以事件发生的频率作为相应事件发生的概率.现从高一、高二年级各随机抽取 1 名家长,记事件:“高一家长的满意度等级高于高二家长的满意度等级”,则事件发生的概率为__________.16.已知函数的图象在处的切线斜率为,则______.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)如图,在直三棱柱中,,点 P,Q 分别为,的中点.求证:(1)PQ平面;(2)平面.18.(12 分)设,函数,其中 为自然对数的底数.(1)设函数.① 若,试判断函数与的图像在区间上是否有交点;② 求证:对任意的,直线都不是的切线;(2)设函数,试判断函数是否存在极小值,若存在,求出的取值范围;若不存在,请说明理由.19.(12 分)如图,在三棱柱中,平面,,且.(1)求棱与所成的角的大小;(2)在棱上确定一点,使二面角的平面角的余弦值为.20.(12 分)已知各项均不相等的等差数列的前项和为, 且成等比数列.(1)求数列的通项公式;(2)求数列的前项和.21.(12 分)如图,底面是等腰梯形,,点为的中点,以为边作正方形,且平面平面.(1)证明:平面平面.(2)求二面角的正弦值.22.(10 分)设首项为 1 的正项数列{an}的前 n 项和为 Sn,数列的前 n 项和为 Tn,且,其中p 为常数.(1)求 p 的值;(2)求证:数列{an}为等比数列;(3)证明:“数列 an,2xan+1,2yan+2成等差数列,其中 x、y 均为整数”的充要条件是“x=1,且 y=2”.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、D【解析】因为,故函数是奇函数,所以排除 A,B;取,则,故选 D.考点:1.函数的基本性质;2.函数的图象.2、B...