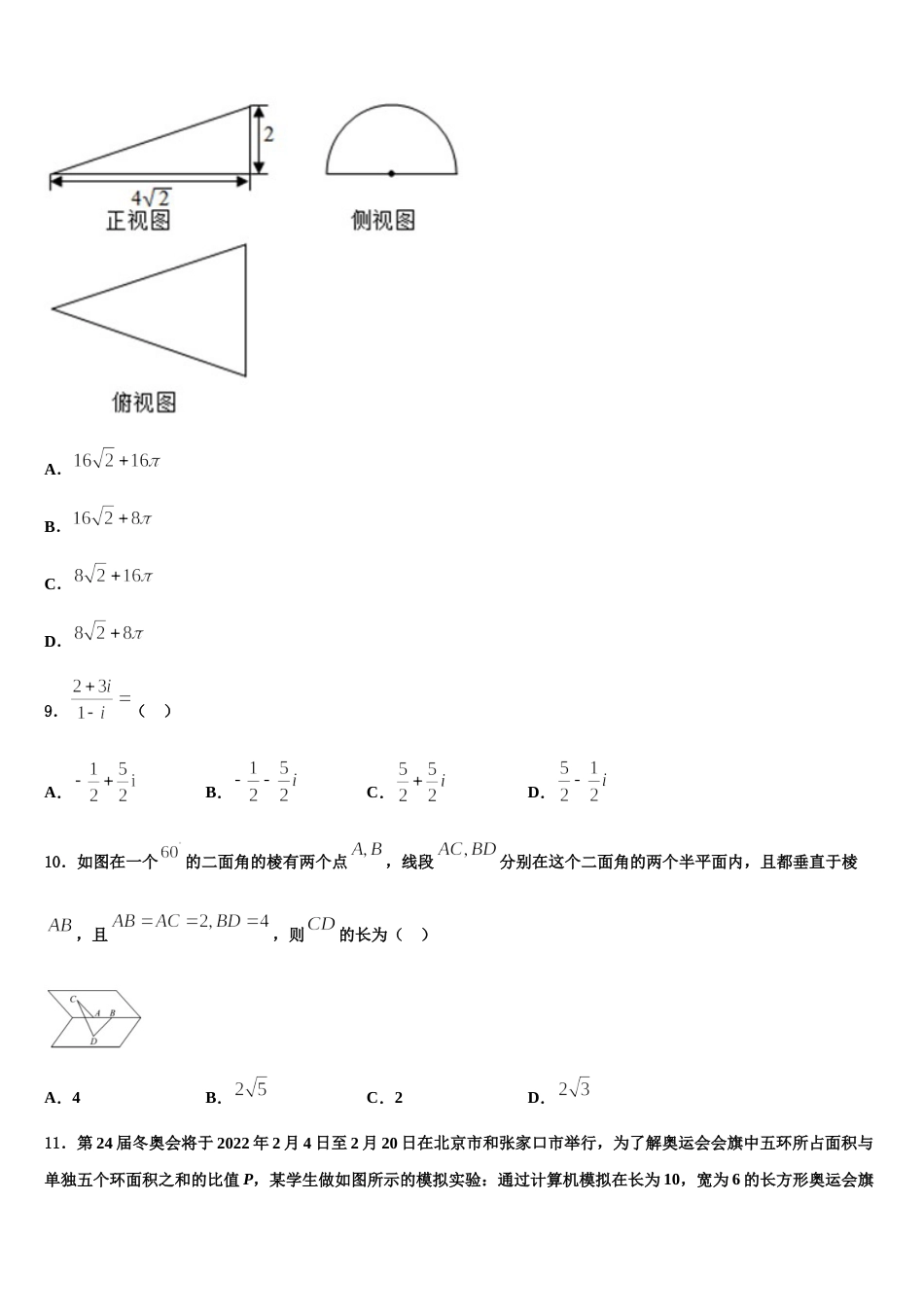
上海师范大学附属中学 2023-2024 学年高三第四次模拟考试数学试卷注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。2.选择题必须使用 2B 铅笔填涂;非选择题必须使用 0.5 毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.《九章算术》勾股章有一“引葭赴岸”问题“今有饼池径丈,葭生其中,出水两尺,引葭赴岸,适与岸齐,问水深,葭各几何?”,其意思是:有一个直径为一丈的圆柱形水池,池中心生有一颗类似芦苇的植物,露出水面两尺,若把它引向岸边,正好与岸边齐,问水有多深,该植物有多高?其中一丈等于十尺,如图若从该葭上随机取一点,则该点取自水下的概率为( )A.B.C.D.2.函数的图象为 C,以下结论中正确的是( )① 图象 C 关于直线对称;② 图象 C 关于点对称;③ 由 y =2sin2x 的图象向右平移个单位长度可以得到图象 C.A.①B.①②C.②③D.①②③3.已知锐角满足则( )A.B.C.D.4.已知三棱锥的所有顶点都在球的球面上,平面,,若球的表面积为,则三棱锥的体积的最大值为( )A.B.C.D.5.下列命题是真命题的是( )A.若平面,,,满足,,则;B.命题:,,则:,;C.“命题为真”是“命题为真”的充分不必要条件;D.命题“若,则”的逆否命题为:“若,则”.6.已知函数,对任意的,,当时,,则下列判断正确的是( )A.B.函数在上递增C.函数的一条对称轴是D.函数的一个对称中心是7.已知函数是定义在上的奇函数,函数满足,且时,,则( )A.2B.C.1D.8.一个几何体的三视图及尺寸如下图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的表面积是 ( ) A.B.C.D.9.( )A.B.C.D.10.如图在一个的二面角的棱有两个点,线段分别在这个二面角的两个半平面内,且都垂直于棱,且,则的长为( )A.4B.C.2D.11.第 24 届冬奥会将于 2022 年 2 月 4 日至 2 月 20 日在北京市和张家口市举行,为了解奥运会会旗中五环所占面积与单独五个环面积之和的比值 P,某学生做如图所示的模拟实验:通过计算机模拟在长为 10,宽为 6 的长方形奥运会旗内随机取 N 个点,经统计落入五环内部及其边界上的点数为 n 个,已知圆环半径为 1,则比值 P 的近似值为( )A.B.C.D.12.已知函数,若有 2 个零点,则实数的取值范围为( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.如图所示梯子结构的点数依次构成数列,则________.14.的展开式中项的系数为_______.15.已知无盖的圆柱形桶的容积是立方米,用来做桶底和侧面的材料每平方米的价格分别为 30 元和 20 元,那么圆桶造价最低为________元.16.如图,在△ABC 中,E 为边 AC 上一点,且,P 为 BE 上一点,且满足,则的最小值为______.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)4 月 23 日是“世界读书日”,某中学开展了一系列的读书教育活动.学校为了解高三学生课外阅读情况,采用分层抽样的方法从高三某班甲、乙、丙、丁四个读书小组(每名学生只能参加一个读书小组)学生抽取 12 名学生参加问卷调查.各组人数统计如下:小组甲乙丙丁人数12969(1)从参加问卷调查的 12 名学生中随机抽取 2 人,求这 2 人来自同一个小组的概率;(2)从已抽取的甲、丙两个小组的学生中随机抽取 2 人,用表示抽得甲组学生的人数,求随机变量的分布列和数学期望.18.(12 分)在平面直角坐标系中,已知椭圆的左、右顶点分别为、,焦距为 2,直线 与椭圆交于两点(均异于椭圆的左、右顶点).当直线 过椭圆的右焦点且垂直于轴时,四边形的面积为...