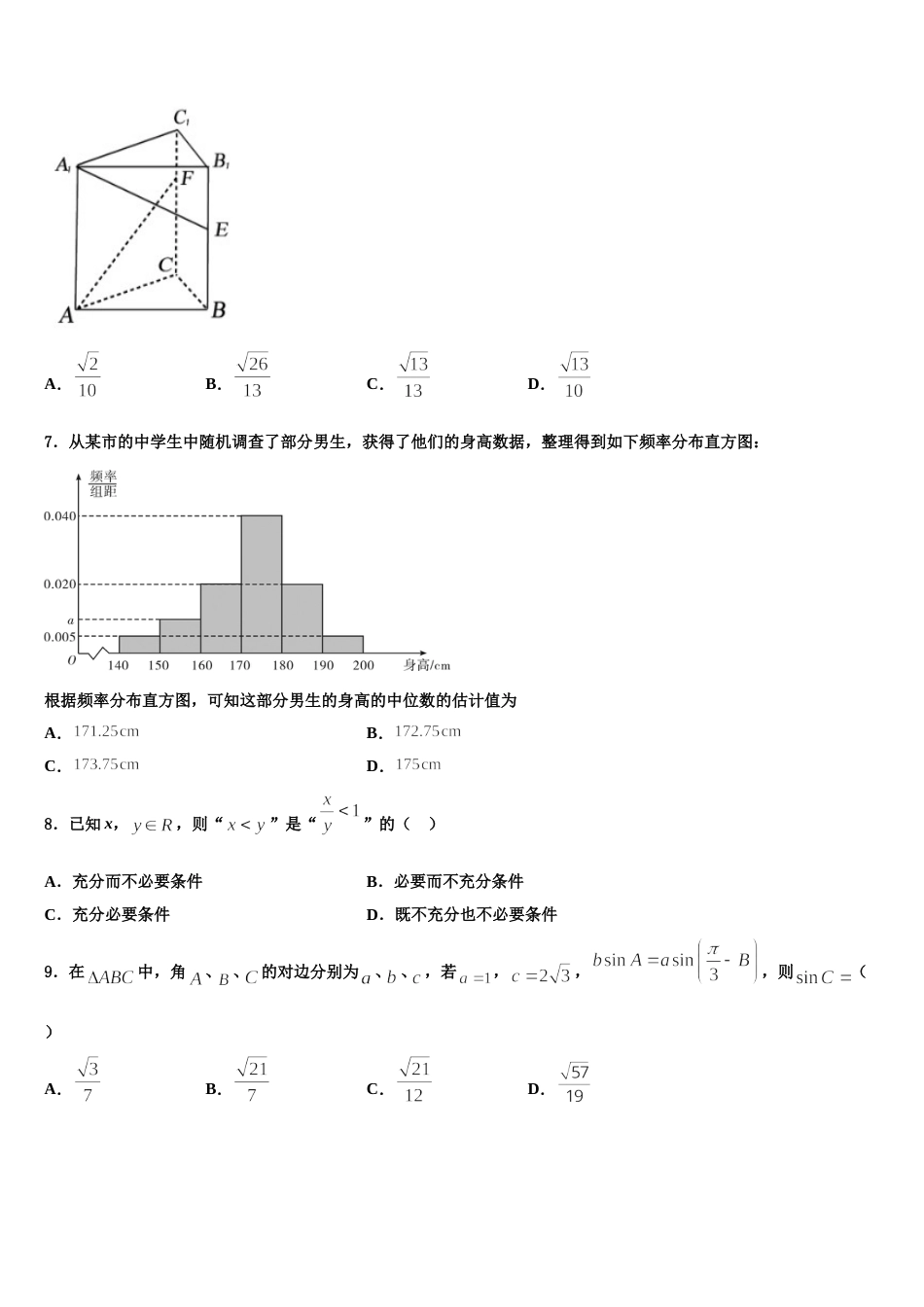
云南楚雄州南华县民中 2024 年高三第三次模拟考试数学试卷注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用 0.5 毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用 2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用 05 毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用 2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.若( 是虚数单位),则的值为( )A.3B.5C.D.2.已知集合,则集合( )A.B.C.D.3.已知变量 x,y 间存在线性相关关系,其数据如下表,回归直线方程为,则表中数据 m 的值为( )变量 x0123变量 y35.57A.0.9B.0.85C.0.75D.0.54.已知复数 z=(1+2i)(1+ai)(a∈R),若 z∈R,则实数 a=( )A.B.C.2D.﹣25.已知函数,,且,则( )A.3B.3 或 7C.5D.5 或 86.如图,在三棱柱中,底面为正三角形,侧棱垂直底面,.若分别是棱上的点,且,,则异面直线与所成角的余弦值为( )A.B.C.D.7.从某市的中学生中随机调查了部分男生,获得了他们的身高数据,整理得到如下频率分布直方图:根据频率分布直方图,可知这部分男生的身高的中位数的估计值为A.B.C.D.8.已知 x,,则“”是“”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件9.在中,角、 、 的对边分别为、 、 ,若,,,则( )A.B.C.D.10.函数的定义域为( )A.[ ,3)∪(3,+∞) B.(-∞,3)∪(3,+∞)C.[ ,+∞) D.(3,+∞)11.一场考试需要 2 小时,在这场考试中钟表的时针转过的弧度数为( )A.B.C.D.12.已知四棱锥的底面为矩形,底面,点在线段上,以为直径的圆过点.若,则的面积的最小值为( )A.9B.7C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.在中,内角的对边长分别为,已知,且,则_________.14.秦九韶算法是南宋时期数学家秦九韶提出的一种多项式简化算法,如图所示的框图给出了利用秦九韶算法求多项式值的一个实例,若输入,的值分別为 4,5,则输出的值为______. 15.已知随机变量服从正态分布,若,则_________.16.一个算法的伪代码如图所示,执行此算法,最后输出的 T 的值为________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知数列和满足:.(1)求证:数列为等比数列;(2)求数列的前项和.18.(12 分)已知函数,其中 e 为自然对数的底数.(1)讨论函数的单调性;(2)用表示中较大者,记函数.若函数在上恰有 2 个零点,求实数 a 的取值范围.19.(12 分)如图,在四棱锥 P-ABCD 中,底面 ABCD 是矩形,PA⊥平面 ABCD,且 PA=AD,E, F 分别是棱 AB,PC 的中点.求证:(1) EF //平面 PAD;(2)平面 PCE⊥平面 PCD.20.(12 分)如图,在四棱锥中底面是菱形,,是边长为的正三角形,,为线段的中点.求证:平面平面;是否存在满足的点,使得?若存在,求出的值;若不存在,请说明理由.21.(12 分)如图,在四棱锥中,底面是边长为 2 的菱形,,平面平面,点为棱的中点.(Ⅰ)在棱上是否存在一点,使得平面,并说明理由;(Ⅱ)当二面角的余弦值为时,求直线与平面所成的角.22.(10 分)表示,中的最大值,如,己知函数,.(1)设,求函数在上的零点个数;(2)试探讨是否存在实数,使得对恒成立?若存在,求的取值范围;若不存在,说明理由.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、D【解析】直接利用复数的模的求法的运算法则求解即可.【详解】( ...