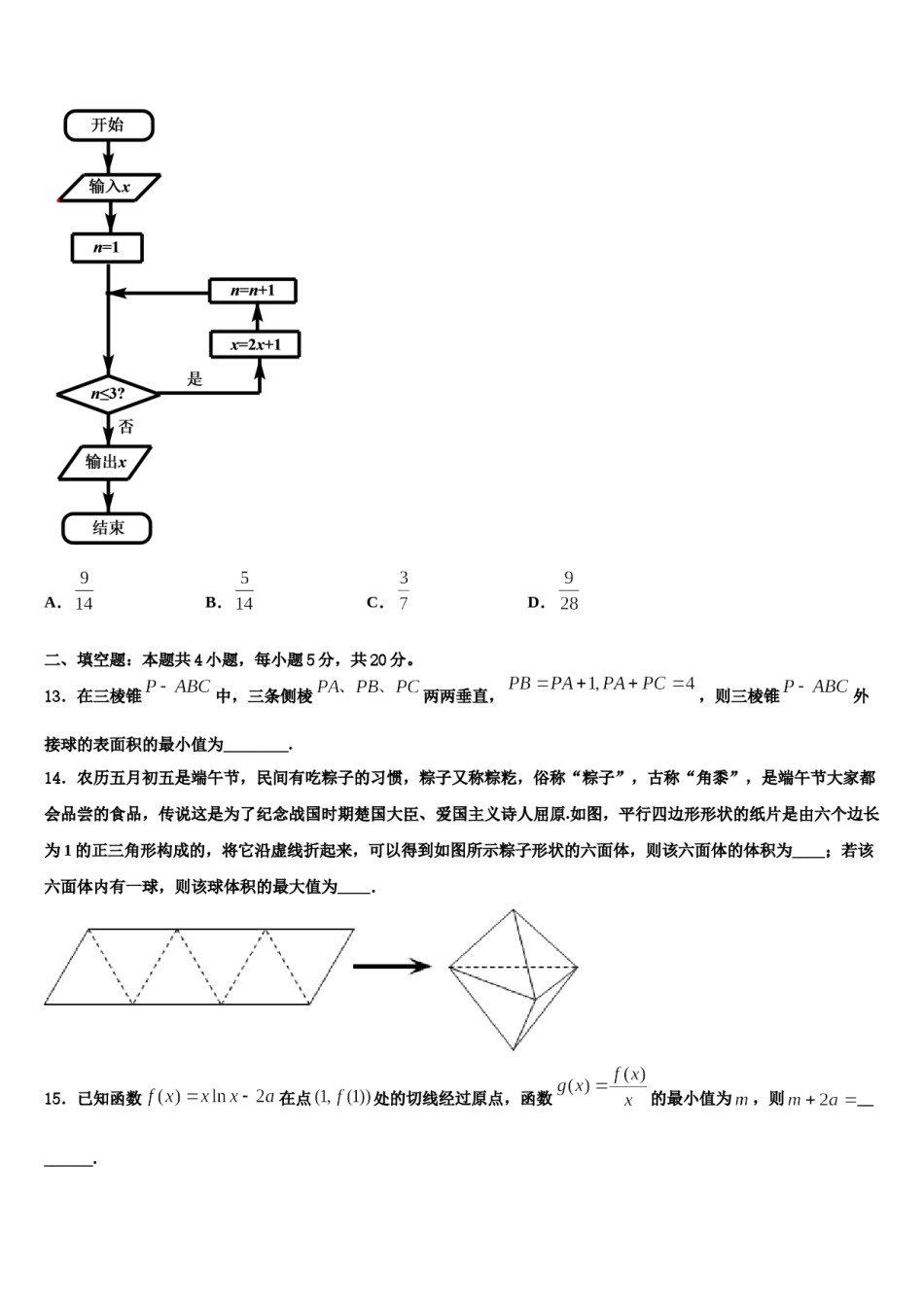
云南省丘北县第一中学2024届高考数学四模试卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知数列的通项公式是,则()A.0B.55C.66D.782.已知,为两条不同直线,,,为三个不同平面,下列命题:①若,,则;②若,,则;③若,,则;④若,,则.其中正确命题序号为()A.②③B.②③④C.①④D.①②③3.已知集合,则()A.B.C.D.4.直线经过椭圆的左焦点,交椭圆于两点,交轴于点,若,则该椭圆的离心率是()A.B.C.D.5.已知复数z满足(i为虚数单位),则在复平面内复数z对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限6.在三角形中,,,求()A.B.C.D.7.已知函数,若,则的最小值为()参考数据:A.B.C.D.8.已知集合A={x–1<x<2},B={xx>1},则A∪B=A.(–1,1)B.(1,2)C.(–1,+∞)D.(1,+∞)9.已知函数,则()A.函数在上单调递增B.函数在上单调递减C.函数图像关于对称D.函数图像关于对称10.已知,则下列说法中正确的是()A.是假命题B.是真命题C.是真命题D.是假命题11.已知椭圆的短轴长为2,焦距为分别是椭圆的左、右焦点,若点为上的任意一点,则的取值范围为()A.B.C.D.12.当输入的实数时,执行如图所示的程序框图,则输出的不小于103的概率是()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.在三棱锥中,三条侧棱两两垂直,,则三棱锥外接球的表面积的最小值为________.14.农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称“粽子”,古称“角黍”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.如图,平行四边形形状的纸片是由六个边长为1的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为____;若该六面体内有一球,则该球体积的最大值为____.15.已知函数在点处的切线经过原点,函数的最小值为,则________.16.若变量,满足约束条件则的最大值为________.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)如图,设A是由个实数组成的n行n列的数表,其中aij(i,j=1,2,3,…,n)表示位于第i行第j列的实数,且aij{1,-1}.记S(n,n)为所有这样的数表构成的集合.对于,记ri(A)为A的第i行各数之积,cj(A)为A的第j列各数之积.令a11a12…a1na21a22a2n…………an1an2…ann(Ⅰ)请写出一个AS(4,4),使得l(A)=0;(Ⅱ)是否存在AS(9,9),使得l(A)=0?说明理由;(Ⅲ)给定正整数n,对于所有的AS(n,n),求l(A)的取值集合.18.(12分)已知函数,当时,有极大值3;(1)求,的值;(2)求函数的极小值及单调区间.19.(12分)已知数列的各项均为正数,为其前n项和,对于任意的满足关系式.(1)求数列的通项公式;(2)设数列的通项公式是,前n项和为,求证:对于任意的正数n,总有.20.(12分)已知,,求证:(1);(2).21.(12分)已知椭圆C:(a>b>0)的两个焦点分别为F1(-,0)、F2(,0).点M(1,0)与椭圆短轴的两个端点的连线相互垂直.(1)求椭圆C的方程;(2)已知点N的坐标为(3,2),点P的坐标为(m,n)(m≠3).过点M任作直线l与椭圆C相交于A、B两点,设直线AN、NP、BN的斜率分别为k1、k2、k3,若k1+k3=2k2,试求m,n满足的关系式.22.(10分)如图,直线与抛物线交于两点,直线与轴交于点,且直线恰好平分.(1)求的值;(2)设是直线上一点,直线交抛物线于另一点,直线交直线于点,求的值.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、D【解析】先分为奇数和偶数两种情况计算出的值,可进一步得...