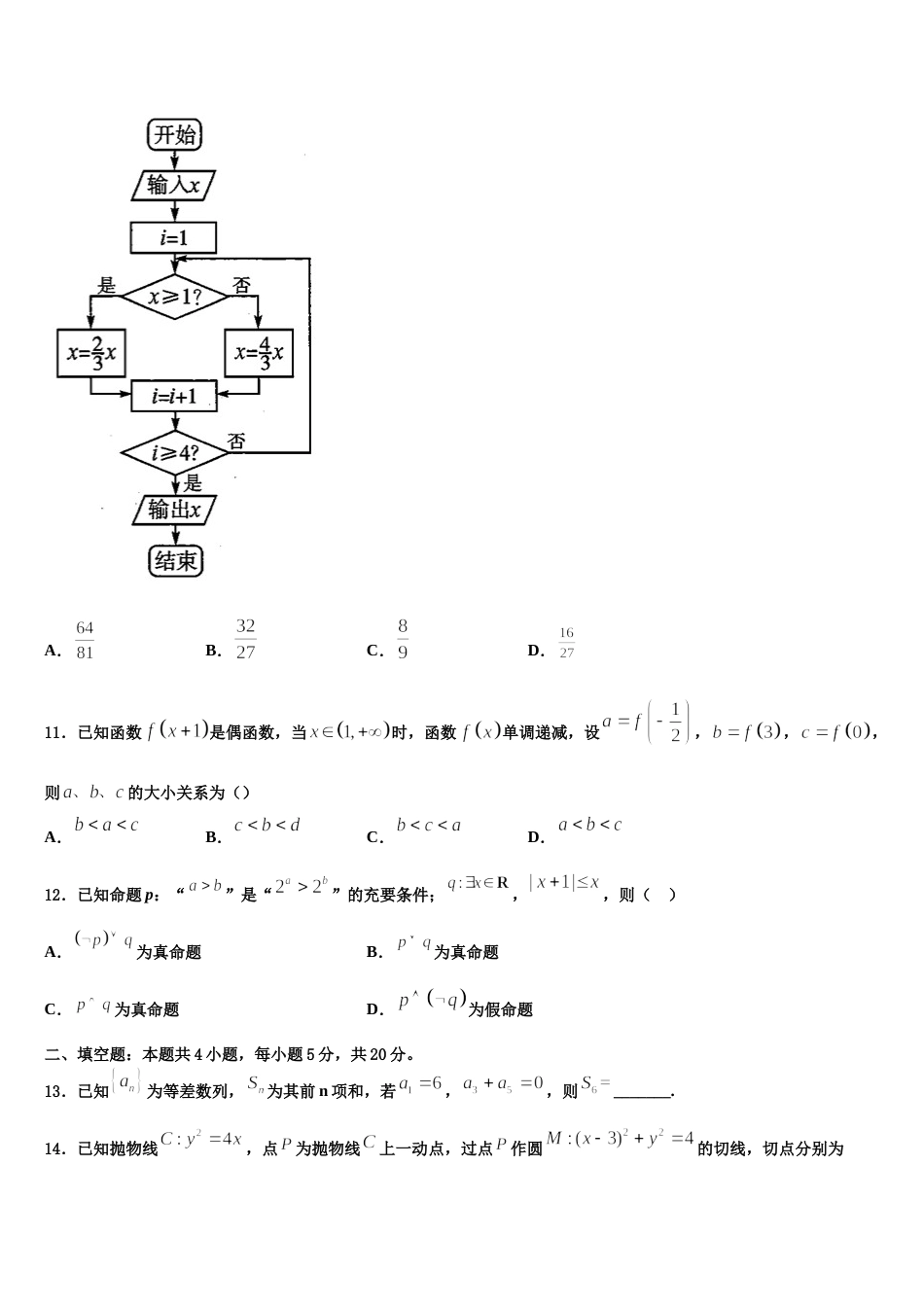
云南省勐腊县第一中学 2024 年高考数学一模试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用 2B 铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。2.作答选择题时,选出每小题答案后,用 2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试题卷上。3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。不按以上要求作答无效。4.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知复数 z 满足,则在复平面上对应的点在( )A.第一象限B.第二象限C.第三象限D.第四象限2.已知三棱锥的外接球半径为 2,且球心为线段的中点,则三棱锥的体积的最大值为( )A.B.C.D.3.已知函数,若关于的不等式恰有 1 个整数解,则实数的最大值为( )A.2B.3C.5D.84.盒中装有形状、大小完全相同的 5 张“刮刮卡”,其中只有 2 张“刮刮卡”有奖,现甲从盒中随机取出 2 张,则至少有一张有奖的概率为( )A.B.C.D.5.已知的内角的对边分别是且,若为最大边,则的取值范围是( )A.B.C.D.6.若,满足约束条件,则的最大值是( )A.B.C.13D.7.已知,则的值等于( )A.B.C.D.8.设双曲线(a>0,b>0)的一个焦点为 F(c,0)(c>0),且离心率等于,若该双曲线的一条渐近线被圆 x2+y22﹣ cx=0 截得的弦长为 2,则该双曲线的标准方程为( )A.B.C.D.9.已知双曲线的一条渐近线与直线垂直,则双曲线的离心率等于( )A.B.C.D.10.相传黄帝时代,在制定乐律时,用“三分损益”的方法得到不同的竹管,吹出不同的音调.如图的程序是与“三分损益”结合的计算过程,若输入的的值为 1,输出的的值为( )A.B.C.D.11.已知函数是偶函数,当时,函数单调递减,设,,,则的大小关系为()A.B.C.D.12.已知命题 p:“”是“”的充要条件;,,则( )A.为真命题B.为真命题C.为真命题D.为假命题二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知为等差数列,为其前 n 项和,若,,则_______.14.已知抛物线,点为抛物线上一动点,过点作圆的切线,切点分别为,则线段长度的取值范围为__________.15.若正实数 , ,满足,则的最大值是__________.16.若复数( 是虚数单位),则________三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)在平面直角坐标系中,曲线:(为参数,),曲线:( 为参数).若曲线和相切.(1)在以为极点,轴非负半轴为极轴的极坐标系中,求曲线的普通方程;(2)若点,为曲线上两动点,且满足,求面积的最大值.18.(12 分)健身馆某项目收费标准为每次 60 元,现推出会员优惠活动:具体收费标准如下:现随机抽取了 100 为会员统计它们的消费次数,得到数据如下:假设该项目的成本为每次 30 元,根据给出的数据回答下列问题:(1)估计 1 位会员至少消费两次的概率(2)某会员消费 4 次,求这 4 次消费获得的平均利润;(3)假设每个会员每星期最多消费 4 次,以事件发生的频率作为相应事件的概率,从会员中随机抽取两位,记从这两位会员的消费获得的平均利润之差的绝对值为,求的分布列及数学期望19.(12 分)如图为某大江的一段支流,岸线与近似满足∥,宽度为.圆为江中的一个半径为的小岛,小镇位于岸线上,且满足岸线,.现计划建造一条自小镇经小岛至对岸的水上通道(图中粗线部分折线段,在右侧),为保护小岛,段设计成与圆相切.设. (1)试将通道的长表示成的函数,并指出定义域;(2)若建造通道的费用是每公里 100 万元,则建造此通道最少需要多少万元?20.(12 分)设函数()的最小值为.(1...