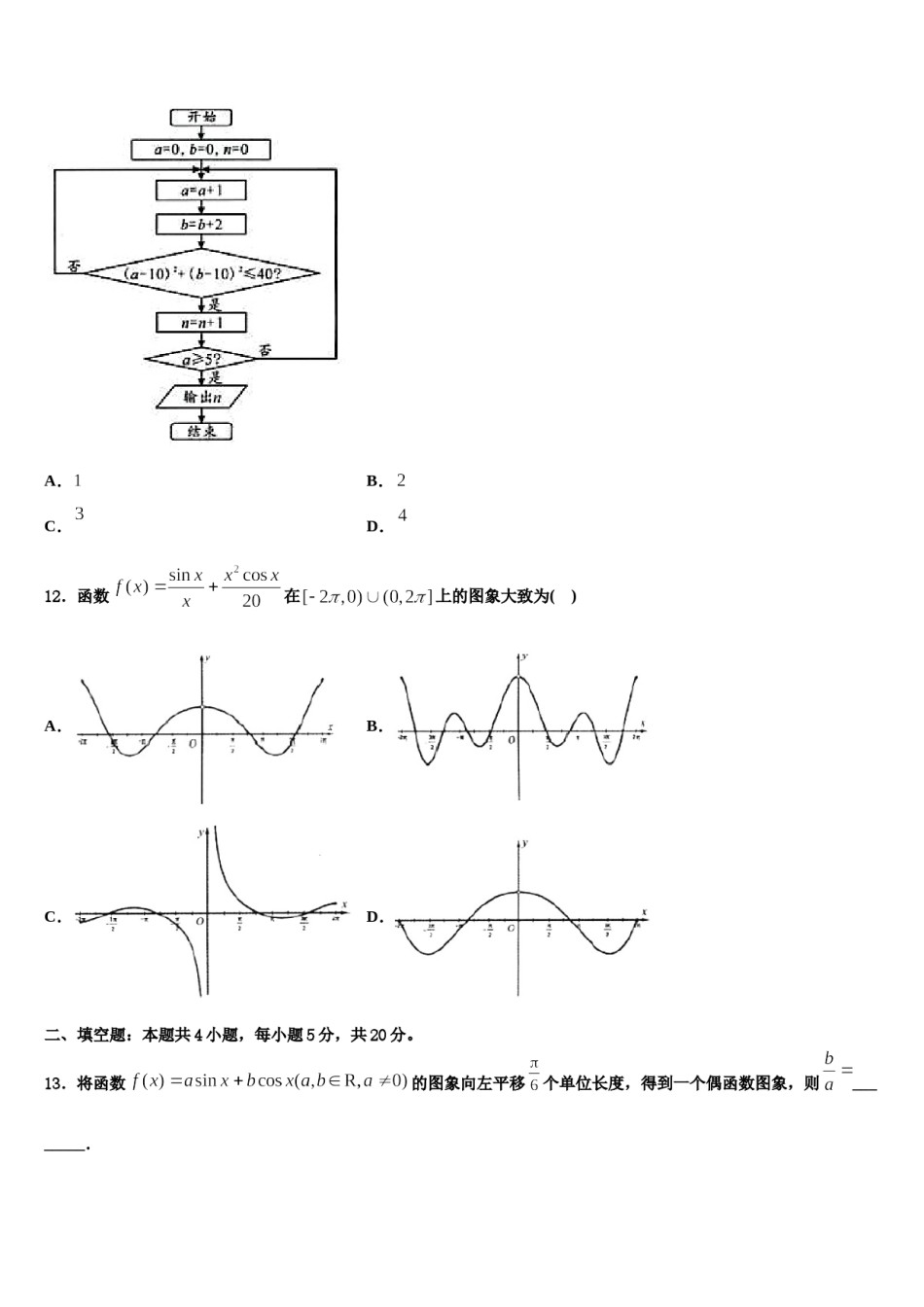
内蒙古呼和浩特市2023-2024学年高三第三次测评数学试卷注意事项铅笔作答;第二部分必须用黑1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.等比数列的前项和为,若,,,,则()A.B.C.D.2.已知,是椭圆与双曲线的公共焦点,是它们的一个公共点,且,椭圆的离心率为,双曲线的离心率为,若,则的最小值为()A.B.C.8D.63.设,则关于的方程所表示的曲线是()A.长轴在轴上的椭圆B.长轴在轴上的椭圆C.实轴在轴上的双曲线D.实轴在轴上的双曲线4.设全集,集合,,则集合()A.B.C.D.5.已知集合,则为()D.(0,2]A.[0,2)B.(2,3]C.[2,3]6.函数的图象如图所示,则它的解析式可能是()A.B.C.D.7.设,满足约束条件,若的最大值为,则的展开式中项的系数为()B.80C.90D.120A.608.复数的共轭复数在复平面内所对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限,若为最大边,则9.已知的内角的对边分别是且的取值范围是()A.B.C.D.10.已知函数,若关于的方程恰好有3个不相等的实数根,则实数的取值范D.围为()A.B.C.11.执行如图所示的程序框图,则输出的的值为()A.B.C.D.12.函数在上的图象大致为()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.将函数的图象向左平移个单位长度,得到一个偶函数图象,则________.14.展开式中项系数为160,则的值为______.15.定义在封闭的平面区域内任意两点的距离的最大值称为平面区域的“直径”.已知锐角三角形的三个点,,,在半径为的圆上,且,分别以各边为直径向外作三个半圆,这三个半圆和构成平面区域,则平面区域的“直径”的最大值是__________.16.在某批次的某种灯泡中,随机抽取200个样品.并对其寿命进行追踪调查,将结果列成频率分布表如下:寿命(天)频数频率40600.30.4200.1合计2001某人从灯泡样品中随机地购买了个,如果这个灯泡的寿命情况恰好与按四个组分层抽样所得的结果相同,则的最小值为______.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知函数.(1)若是的极值点,求的极大值;(2)求实数的范围,使得恒成立.18.(12分)已知等差数列{an}的各项均为正数,Sn为等差数列{an}的前n项和,.,侧(1)求数列{an}的通项an;(2)设bn=an⋅3n,求数列{bn}的前n项和Tn.19.(12分)如图,三棱柱中,与均为等腰直角三角形,面是菱形.(1)证明:平面平面;(2)求二面角的余弦值.20.(12分)管道清洁棒是通过在管道内释放清洁剂来清洁管道内壁的工具,现欲用清洁棒清洁一个如图1所示的圆管直角弯头的内壁,其纵截面如图2所示,一根长度为的清洁棒在弯头内恰好处于位置(图中给出的数据是圆管内壁直径大小,).(1)请用角表示清洁棒的长;(2)若想让清洁棒通过该弯头,清洁下一段圆管,求能通过该弯头的清洁棒的最大长度.21.(12分)已知函数和的图象关于原点对称,且.(1)解关于的不等式;恒成立,求实数的取值范围.(2)如果对,不等式22.(10分)设椭圆:的右焦点为,右顶点为,已知椭圆离心率为,过点且与轴垂直的直线被椭圆截得的线段长为3.(Ⅰ)求椭圆的方程;(Ⅱ)设过点的直线与椭圆交于点(不在轴上),垂直于的直线与交于点,与轴交于点,若,且,求直线斜率的取值范围.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、D【解析】试题分析:由于在等比数列中,由可得:,又因为,所以有:是方程的二实根,又,,所以,故解得:,从而公比;那么,故选D.考点:等比数列.2、C【解析】由椭圆的定义以及双曲线的定义、离心率公式化简,结合基本不等式即可求解.【详解】设椭圆的长半轴长为,双曲线的半实轴长为,半焦距为,则,,设由椭圆的定义以及双曲线的定义可得...