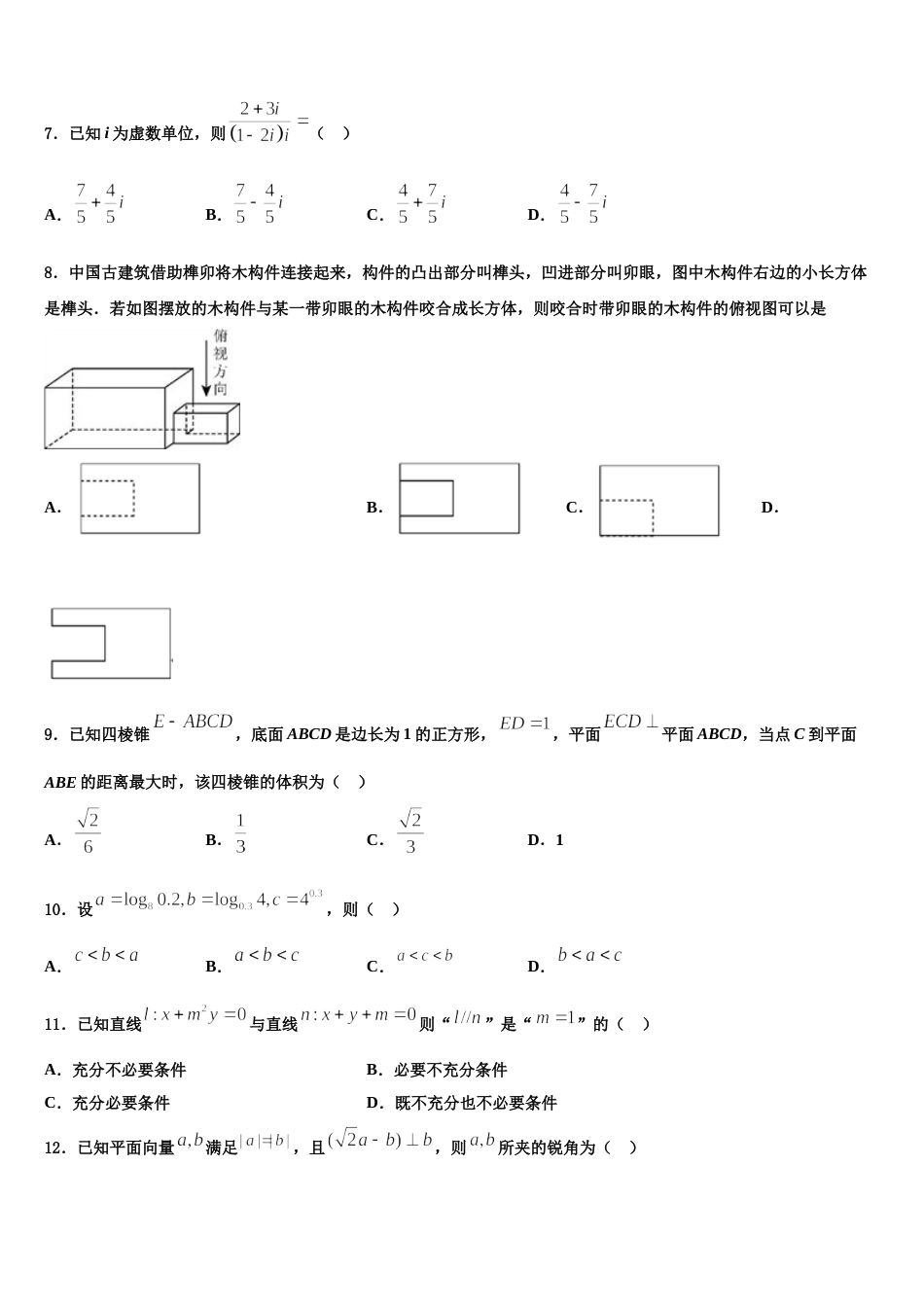
内蒙古巴彦淖尔市第一中学 2024 年高三适应性调研考试数学试题注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知三棱锥且平面,其外接球体积为( )A.B.C.D.2.若函数有两个极值点,则实数的取值范围是( )A.B.C.D.3.已知数列是公差为的等差数列,且成等比数列,则( )A.4B.3C.2D.14.某装饰公司制作一种扇形板状装饰品,其圆心角为 120°,并在扇形弧上正面等距安装 7 个发彩色光的小灯泡且在背面用导线相连(弧的两端各一个,导线接头忽略不计),已知扇形的半径为 30 厘米,则连接导线最小大致需要的长度为( )A.58 厘米B.63 厘米C.69 厘米D.76 厘米5. 下列与的终边相同的角的表达式中正确的是( )A.2kπ+45°(k∈Z)B.k·360°+ π(kZ)∈C.k·360°-315°(k∈Z)D.kπ+ (kZ)∈6.三棱锥的各个顶点都在求的表面上,且是等边三角形,底面,,,若点在线段上,且,则过点的平面截球所得截面的最小面积为( )A.B.C.D.7.已知 i 为虚数单位,则( )A.B.C.D.8.中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是A.B.C.D.9.已知四棱锥,底面 ABCD 是边长为 1 的正方形,,平面平面 ABCD,当点 C 到平面ABE 的距离最大时,该四棱锥的体积为( )A.B.C.D.110.设,则( )A.B.C.D.11.已知直线与直线则“”是“”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件12.已知平面向量满足,且,则所夹的锐角为( )A.B.C.D.0二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知,在方向上的投影为,则与的夹角为_________.14.直线 xsinα+y+2=0 的倾斜角的取值范围是________________.15.已知椭圆的左、右焦点分别为、,过椭圆的右焦点作一条直线 交椭圆于点、.则内切圆面积的最大值是_________.16.已知 F 为抛物线 C:x2=8y 的焦点,P 为 C 上一点,M(﹣4,3),则△PMF 周长的最小值是_____.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知函数,其中.(1)讨论函数的零点个数;(2)求证:.18.(12 分)已知函数.其中 是自然对数的底数.(1)求函数在点处的切线方程;(2)若不等式对任意的恒成立,求实数的取值范围.19.(12 分)如图,在四棱锥中,底面是边长为 2 的菱形,,.(1)证明:平面平面 ABCD;(2)设 H 在 AC 上,,若,求 PH 与平面 PBC 所成角的正弦值.20.(12 分)设,,其中.(1)当时,求的值;(2)对,证明:恒为定值.21.(12 分)已知关于的不等式有解.(1)求实数的最大值 ;(2)若,,均为正实数,且满足.证明:.22.(10 分)已知函数(,)满足下列 3 个条件中的 2 个条件:① 函数的周期为;②是函数的对称轴;③且在区间上单调.(Ⅰ)请指出这二个条件,并求出函数的解析式;(Ⅱ)若,求函数的值域.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、A【解析】由,平面,可将三棱锥还原成长方体,则三棱锥的外接球即为长方体的外接球,进而求解.【详解】由题,因为,所以,设,则由,可得,解得,可将三棱锥还原成如图所示的长方体,则三棱锥的外接球即为长方体的外接球,设外接球的半径为,则,所以,所以外接球的体积.故选:A【点睛】本题考查三棱锥的外接球体积,考查空间想象能力.2、A【解析】试题分析:由题意得有两个...