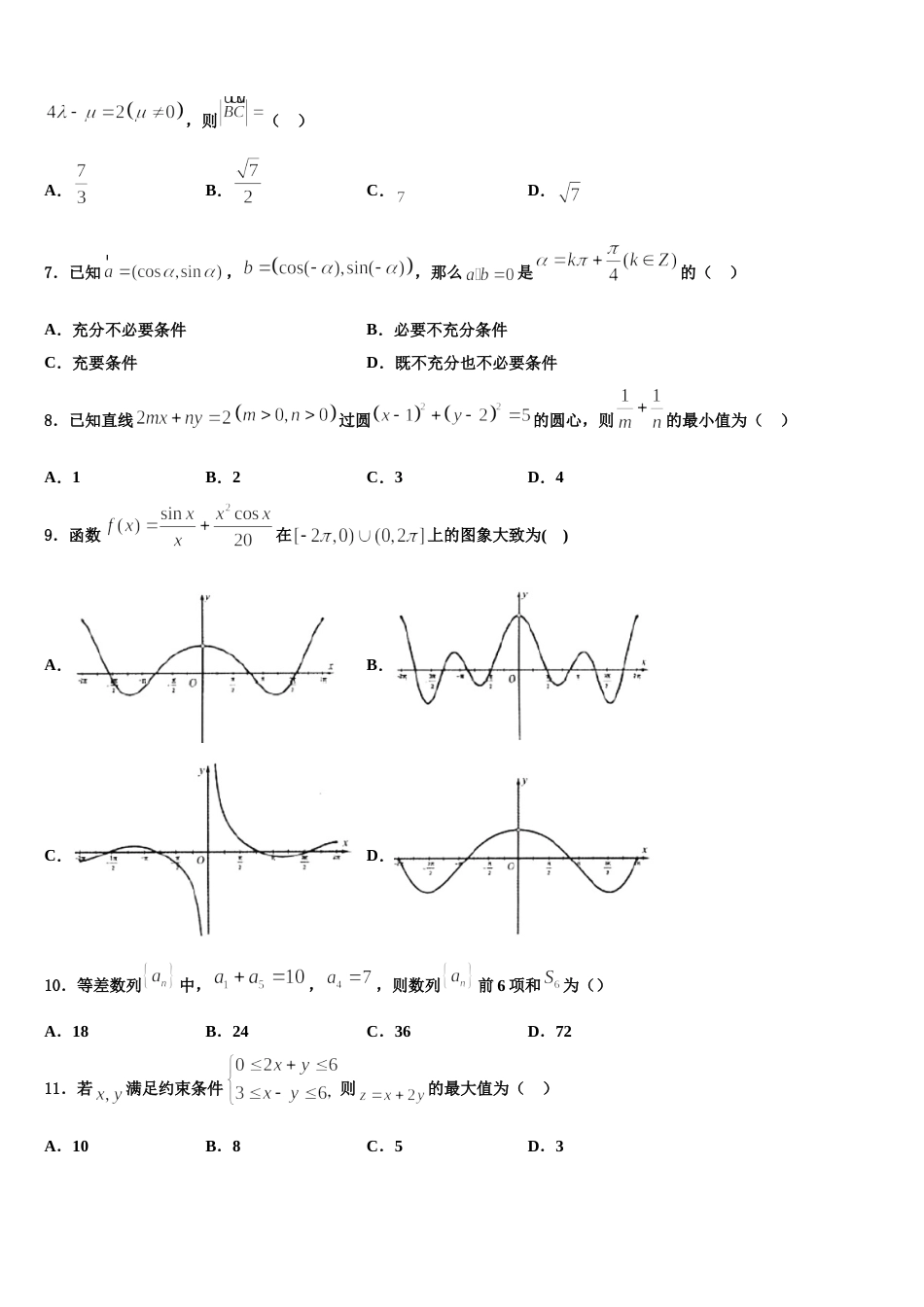
北京市二十二中 2024 届高三第一次模拟考试数学试卷请考生注意:1.请用 2B 铅笔将选择题答案涂填在答题纸相应位置上,请用 0.5 毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知集合 A={y|y=|x|1﹣ ,x∈R},B={x|x≥2},则下列结论正确的是( )A.﹣3∈A B.3B C.A∩B=B D.AB=B∪2.已知函数(其中 为自然对数的底数)有两个零点,则实数的取值范围是( )A.B.C.D.3.若将函数的图象上各点横坐标缩短到原来的(纵坐标不变)得到函数的图象,则下列说法正确的是( )A.函数在上单调递增B.函数的周期是C.函数的图象关于点对称D.函数在上最大值是 14.已知集合 A={x∈N|x2<8x},B={2,3,6},C={2,3,7},则=( )A.{2,3,4,5}B.{2,3,4,5,6}C.{1,2,3,4,5,6}D.{1,3,4,5,6,7}5.若复数满足,则( )A.B.C.D.6.点在所在的平面内,,,,,且,则( )A.B.C.D.7.已知,,那么是的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件8.已知直线过圆的圆心,则的最小值为( )A.1B.2C.3D.49.函数在上的图象大致为( )A.B.C.D.10.等差数列中,,,则数列前 6 项和为()A.18B.24C.36D.7211.若满足约束条件则的最大值为( )A.10B.8C.5D.312.已知三点 A(1,0),B(0, ),C(2,),则△ABC 外接圆的圆心到原点的距离为( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.在中,为定长,,若的面积的最大值为,则边的长为____________.14.已知数列满足对任意,若,则数列的通项公式________.15.如图,在棱长为 2 的正方体中,点、分别是棱,的中点,是侧面正方形内一点(含边界),若平面,则线段长度的取值范围是______.16.若在上单调递减,则的取值范围是_______三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)百年大计,教育为本.某校积极响应教育部号召,不断加大拔尖人才的培养力度,为清华、北大等排名前十的名校输送更多的人才.该校成立特长班进行专项培训.据统计有如下表格.(其中表示通过自主招生获得降分资格的学生人数,表示被清华、北大等名校录取的学生人数)年份(届)2014201520162017201841495557638296108106123(1)通过画散点图发现与之间具有线性相关关系,求关于的线性回归方程;(保留两位有效数字)(2)若已知该校 2019 年通过自主招生获得降分资格的学生人数为 61 人,预测 2019 年高考该校考人名校的人数;(3)若从 2014 年和 2018 年考人名校的学生中采用分层抽样的方式抽取出 5 个人回校宣传,在选取的 5 个人中再选取2 人进行演讲,求进行演讲的两人是 2018 年毕业的人数的分布列和期望.参考公式:,参考数据:,,,18.(12 分)已知椭圆的右焦点为,直线被称作为椭圆的一条准线,点在椭圆上(异于椭圆左、右顶点),过点作直线与椭圆相切,且与直线 相交于点.(1)求证:.(2)若点在轴的上方,当的面积最小时,求直线的斜率.附:多项式因式分解公式:19.(12 分)已知的内角,,的对边分别为,,,且.(1)求;(2)若的面积为,,求的周长.20.(12 分)已知是圆:的直径,动圆过,两点,且与直线相切.(1)若直线的方程为,求的方程;(2)在轴上是否存在一个定点,使得以为直径的圆恰好与轴相切?若存在,求出点的坐标;若不存在,请说明理由.21.(12 分)已知函数.(1)求不等式的解集;(2)若不等式在上恒成立,求实数的取值范围.22.(10 分)如图,在四棱锥中,,,,和均为边长为的等边三角形.(1)求证:平面平面;(2)求二面角的余弦值.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、C【解析】试题...