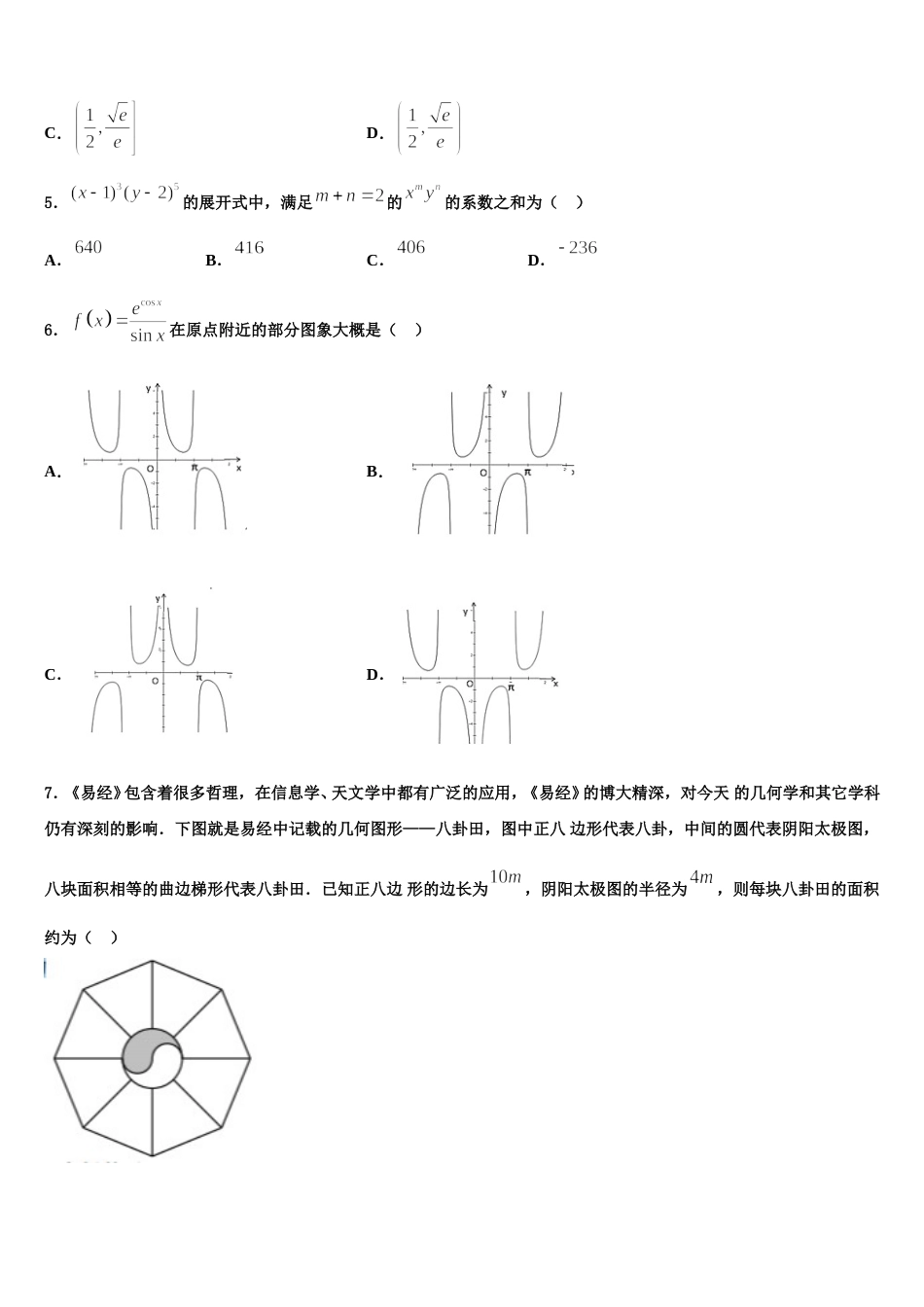
北京市石景山区 2023-2024 学年高三下学期第六次检测数学试卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.等差数列中,,,则数列前 6 项和为()A.18B.24C.36D.722.双曲线的渐近线方程为( )A.B.C.D.3.阅读如图的程序框图,运行相应的程序,则输出的的值为( )A.B.C.D.4.已知函数 f(x)=,若关于 x 的方程 f(x)=kx-恰有 4 个不相等的实数根,则实数 k 的取值范围是( )A. B. C. D. 5.的展开式中,满足的的系数之和为( )A.B.C.D.6.在原点附近的部分图象大概是( )A.B.C.D.7.《易经》包含着很多哲理,在信息学、天文学中都有广泛的应用,《易经》的博大精深,对今天 的几何学和其它学科仍有深刻的影响.下图就是易经中记载的几何图形——八卦田,图中正八 边形代表八卦,中间的圆代表阴阳太极图,八块面积相等的曲边梯形代表八卦田.已知正八边 形的边长为,阴阳太极图的半径为,则每块八卦田的面积约为( )A.B.C.D.8.关于的不等式的解集是,则关于的不等式的解集是( )A.B.C.D.9.设,则( )A.B.C.D.10.某个命题与自然数有关,且已证得“假设时该命题成立,则时该命题也成立”.现已知当时,该命题不成立,那么( )A.当时,该命题不成立B.当时,该命题成立C.当时,该命题不成立D.当时,该命题成立11.已知正项等比数列的前项和为,则的最小值为( )A.B.C.D.12.《九章算术》中记载,堑堵是底面为直角三角形的直三棱柱,阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵中,,,当阳马体积的最大值为时,堑堵的外接球的体积为( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.若函数 (R,)满足,且的最小值等于,则 ω 的值为___________.14.如图,、分别是双曲线的左、右焦点,过的直线与双曲线的两条渐近线分别交于、两点,若,,则双曲线的离心率是______.15.设为定义在上的偶函数,当时,(为常数),若,则实数的值为______.16.如图,已知扇形的半径为 1,面积为,则_____.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知函数.(1)解不等式;(2)若函数存在零点,求的求值范围.18.(12 分)已知函数,设为的导数,.(1)求,; (2)猜想的表达式,并证明你的结论.19.(12 分)椭圆的左、右焦点分别为,椭圆上两动点使得四边形为平行四边形,且平行四边形的周长和最大面积分别为 8 和.(1)求椭圆的标准方程;(2)设直线与椭圆的另一交点为,当点在以线段为直径的圆上时,求直线的方程.20.(12 分)如图,已知,分别是正方形边,的中点,与交于点,,都垂直于平面,且,,是线段上一动点.(1)当平面,求的值;(2)当是中点时,求四面体的体积.21.(12 分)如图,正方形是某城市的一个区域的示意图,阴影部分为街道,各相邻的两红绿灯之间的距离相等,处为红绿灯路口,红绿灯统一设置如下:先直行绿灯 30 秒,再左转绿灯 30 秒,然后是红灯 1 分钟,右转不受红绿灯影响,这样独立的循环运行.小明上学需沿街道从处骑行到处(不考虑处的红绿灯),出发时的两条路线()等可能选择,且总是走最近路线.(1)请问小明上学的路线有多少种不同可能?(2)在保证通过红绿灯路口用时最短的前提下,小明优先直行,求小明骑行途中恰好经过处,且全程不等红绿灯的概率;(3)请你根据每条可能的路线中等红绿灯的次数的均值,为小明设计一条最佳的上学路线,且应尽量避开哪条路线?22.(10 分)如图,⊙的直径的延长线与弦的延长线相交于点,为⊙上一点,,交于点.求证:~.参考答案一、选择题:本...