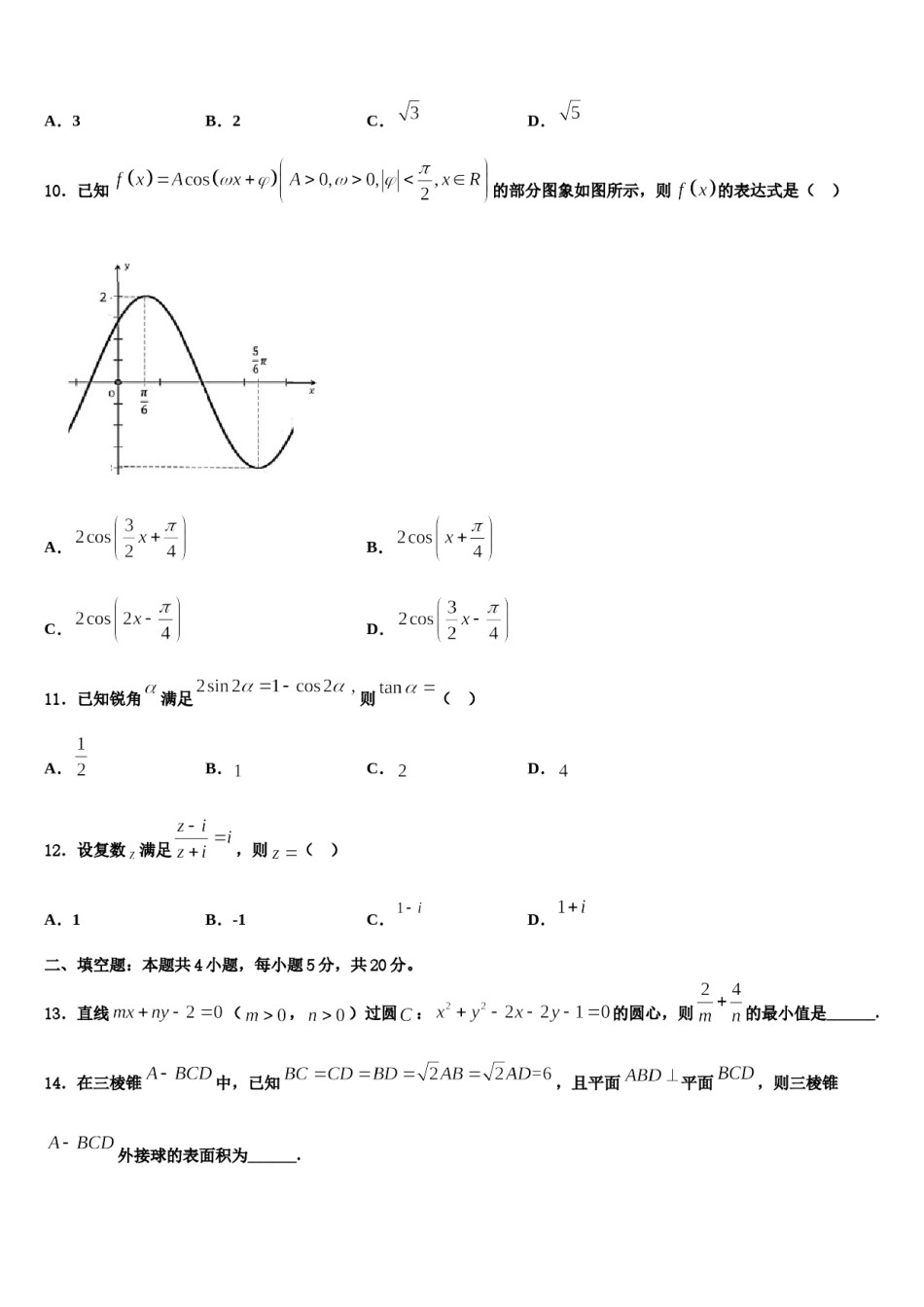
北京市西城区第一五六中学2024届高考仿真卷数学试题考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.若函数(其中,图象的一个对称中心为,,其相邻一条对称轴方程为,该对称轴处所对应的函数值为,为了得到的图象,则只要将的图象()A.向右平移个单位长度B.向左平移个单位长度C.向左平移个单位长度D.向右平移个单位长度2.执行如图所示的程序框图,则输出的的值是()A.8B.32C.64D.1283.若数列,则使的的值为()满足且A.B.C.D.4.一个四面体所有棱长都是4,四个顶点在同一个球上,则球的表面积为()A.B.C.D.5.已知为虚数单位,复数,则其共轭复数()A.B.C.D.6.已知,,,则()A.B.C.D.7.上世纪末河南出土的以鹤的尺骨(翅骨)制成的“骨笛”(图1),充分展示了我国古代高超的音律艺术及先进的数学水平,也印证了我国古代音律与历法的密切联系.图2为骨笛测量“春(秋)分”,“夏(冬)至”的示意图,图3是某骨笛的部分测量数据(骨笛的弯曲忽略不计),夏至(或冬至)日光(当日正午太阳光线)与春秋分日光(当日正午太阳光线)的夹角等于黄赤交角.由历法理论知,黄赤交角近1万年持续减小,其正切值及对应的年代如下表:黄赤交角正切值0.4390.4440.4500.4550.461年代公元元年公元前2000年公元前4000年公元前6000年公元前8000年根据以上信息,通过计算黄赤交角,可估计该骨笛的大致年代是()A.公元前2000年到公元元年B.公元前4000年到公元前2000年C.公元前6000年到公元前4000年D.早于公元前6000年8.已知定点都在平面内,定点是内异于的动点,且,那么动点在平面内的轨迹是()B.椭圆,但要去掉两个点A.圆,但要去掉两个点D.抛物线,但要去掉两个点C.双曲线,但要去掉两个点9.已知是圆心为坐标原点,半径为1的圆上的任意一点,将射线绕点逆时针旋转到交圆于点,则的最大值为()A.3B.2C.D.10.已知的部分图象如图所示,则的表达式是()A.B.C.D.11.已知锐角满足则()A.B.C.D.12.设复数满足,则()A.1B.-1C.D.二、填空题:本题共4小题,每小题5分,共20分。13.直线(,)过圆:的圆心,则的最小值是______.14.在三棱锥中,已知,且平面平面,则三棱锥外接球的表面积为______.15.函数过定点________.16.已知集合,,则____________.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知函数.(1)当时,求曲线在点处的切线方程;(2)若在上恒成立,求的取值范围.18.(12分)班主任为了对本班学生的考试成绩进行分析,决定从本班24名女同学,18名男同学中随机抽取一个容量为7的样本进行分析.(1)如果按照性别比例分层抽样,可以得到多少个不同的样本?(写出算式即可,不必计算出结果)(2)如果随机抽取的7名同学的数学,物理成绩(单位:分)对应如下表:学生序号1234567数学成绩60657075858790物理成绩70778085908693①若规定85分以上(包括85分)为优秀,从这7名同学中抽取3名同学,记3名同学中数学和物理成绩均为优秀的人数为,求的分布列和数学期望;②根据上表数据,求物理成绩关于数学成绩的线性回归方程(系数精确到0.01);若班上某位同学的数学成绩为96分,预测该同学的物理成绩为多少分?附:线性回归方程,其中,.768381252619.(12分)已知函数.若在定义域内存在,使得成立,则称为函数的局部对称点.且a≠0,证明:函数有局部对称点;(1)若a,(2)若函数在定义域内有局部对称点,求实数c的取值范围;(3)若函数在R上有局部对称点,求实数m的取值范围.20.(12分)P是圆上的动点,P点在x轴上的射影是D,点M满足.(1)求动点M的轨迹C的方程,并说明轨迹是什么图形;(2)过点的直线l与动点M的轨迹...