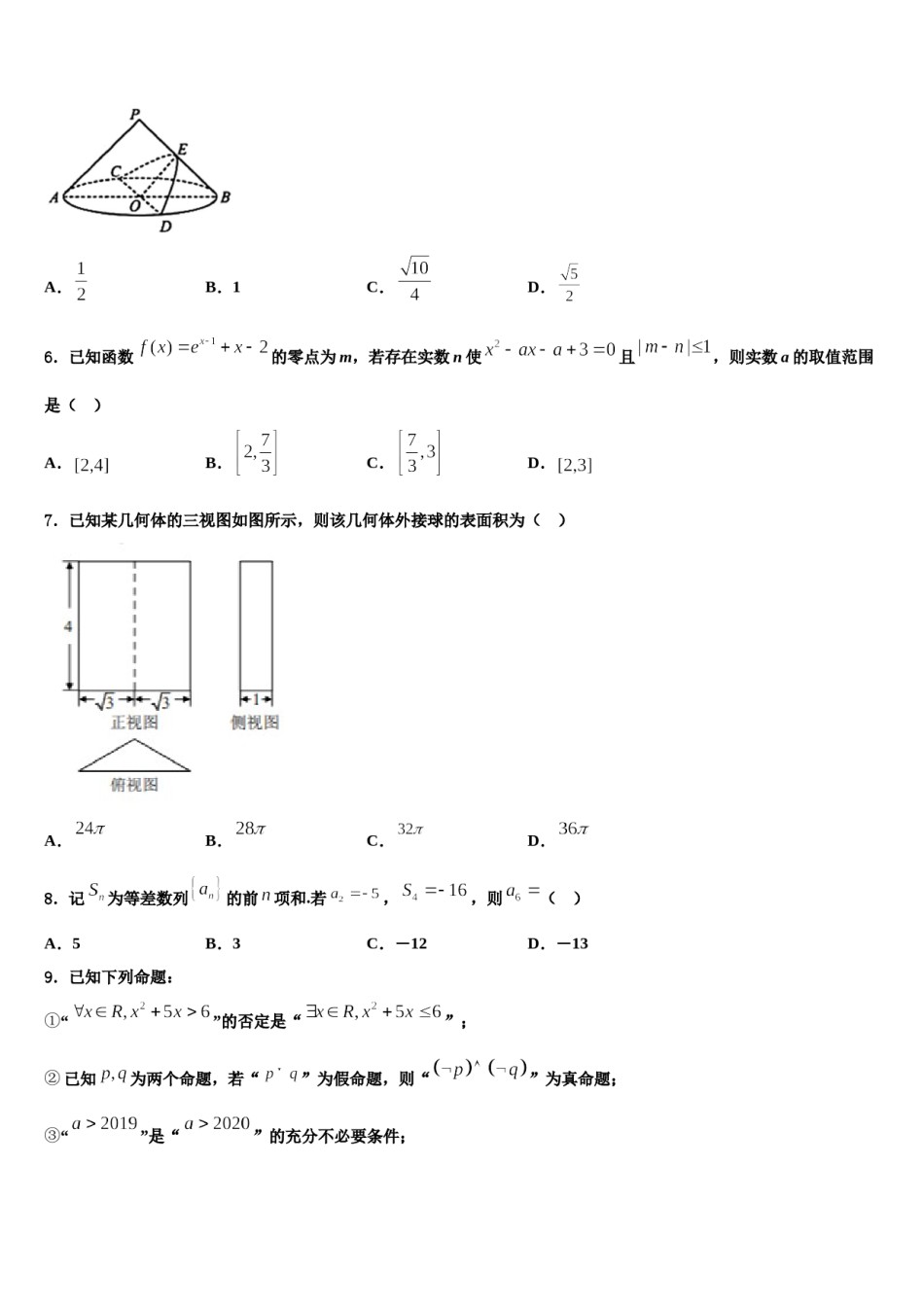
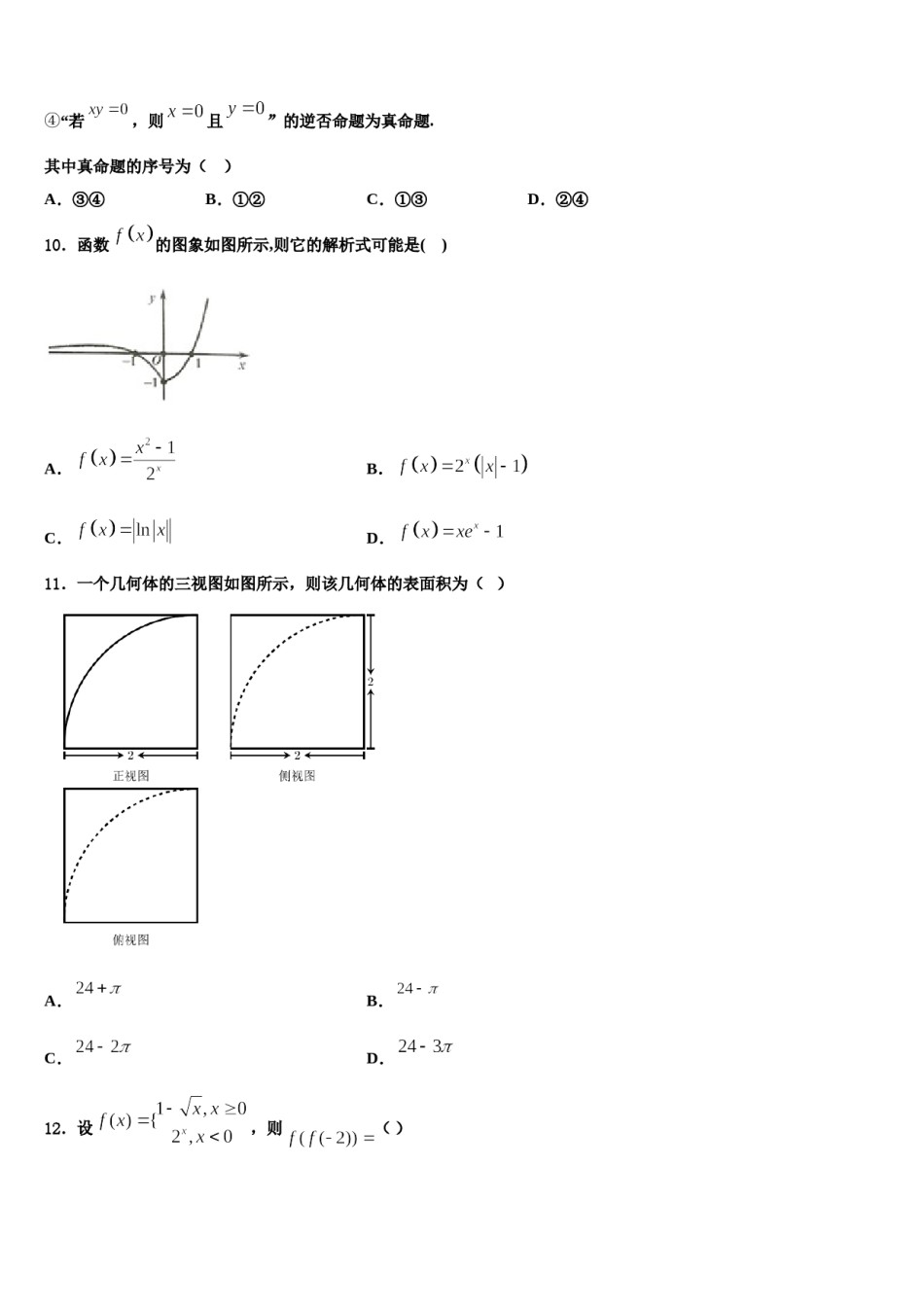
吉安一中2024年高三第四次模拟考试数学试卷请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知函数,若,则a的取值范围为()A.B.C.D.2.下列函数中,在区间上为减函数的是()A.B.C.D.3.设,是方程的两个不等实数根,记().下列两个命题()①数列的任意一项都是正整数;②数列存在某一项是5的倍数.A.①正确,②错误B.①错误,②正确C.①②都正确D.①②都错误4.在中,,则()A.B.C.D.5.如图,圆锥底面半径为,体积为,、是底面圆的两条互相垂直的直径,是母线的中点,已知过与的平面与圆锥侧面的交线是以为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点的距离等于()A.B.1C.D.6.已知函数的零点为m,若存在实数n使且,则实数a的取值范围是()A.B.C.D.7.已知某几何体的三视图如图所示,则该几何体外接球的表面积为()A.B.C.D.8.记为等差数列的前项和.若,,则()C.-12D.-13A.5B.39.已知下列命题:①“”的否定是“”;②已知为两个命题,若“”为假命题,则“”为真命题;③“”是“”的充分不必要条件;④“若,则且”的逆否命题为真命题.其中真命题的序号为()A.③④B.①②C.①③D.②④10.函数的图象如图所示,则它的解析式可能是()A.B.C.D.11.一个几何体的三视图如图所示,则该几何体的表面积为()A.B.C.D.12.设,则()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.在的展开式中,所有的奇数次幂项的系数和为-64,则实数的值为__________.14.已知,为双曲线的左、右焦点,双曲线的渐近线上存在点满足,则的最大值为________.15.设等差数列的前项和为,若,,则数列的公差________,通项公式_____的___.16.等差数列(公差不为0),其中,,成等比数列,则这个等比数列的公比为_____.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知函数.若在定义域内存在,使得成立,则称为函数局部对称点.且a≠0,证明:函数有局部对称点;(1)若a,(2)若函数在定义域内有局部对称点,求实数c的取值范围;(3)若函数在R上有局部对称点,求实数m的取值范围.18.(12分)设数列是等比数列,,已知,(1)求数列的首项和公比;(2)求数列的通项公式.是减函数.19.(12分)已知函数(1)试确定a的值;,求证:.(2)已知数列20.(12分)已知等差数列的前n项和为,且,.求数列的通项公式;求数列的前n项和.21.(12分)在中,角、、的对边分别为、、,且.(1)若,,求的值;(2)若,求的值.22.(10分)在直角坐标系中,已知点,的参数方程为(为参数),以坐标原点为极点,轴的正半轴为极轴,建立极坐标系,曲线的极坐标方程为.(1)求的普通方程和的直角坐标方程;(2)设曲线与曲线相交于,两点,求的值.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、C【解析】求出函数定义域,在定义域内确定函数的单调性,利用单调性解不等式.【详解】由得,在时,是增函数,是增函数,是增函数,∴是增函数,∴由得,解得.故选:C.【点睛】本题考查函数的单调性,考查解函数不等式,解题关键是确定函数的单调性,解题时可先确定函数定义域,在定义域内求解.2、C【解析】利用基本初等函数的单调性判断各选项中函数在区间上的单调性,进而可得出结果.【详解】对于A选项,函数在区间上为增函数;对于B选项,函数在区间上为增函数;对于C选项,函数在区间上为减函数;对于D选项,函数在区间上为增函数.故选:C.【点睛】本题考查函数在区间上单调性的判断,熟悉一些常见的基本初等函数的单调性是判断的关键,属于基础题.3、A【解析】利用韦达定理可得,,结合可推出,再计算出,,从而推出①正确;再利用递推公...