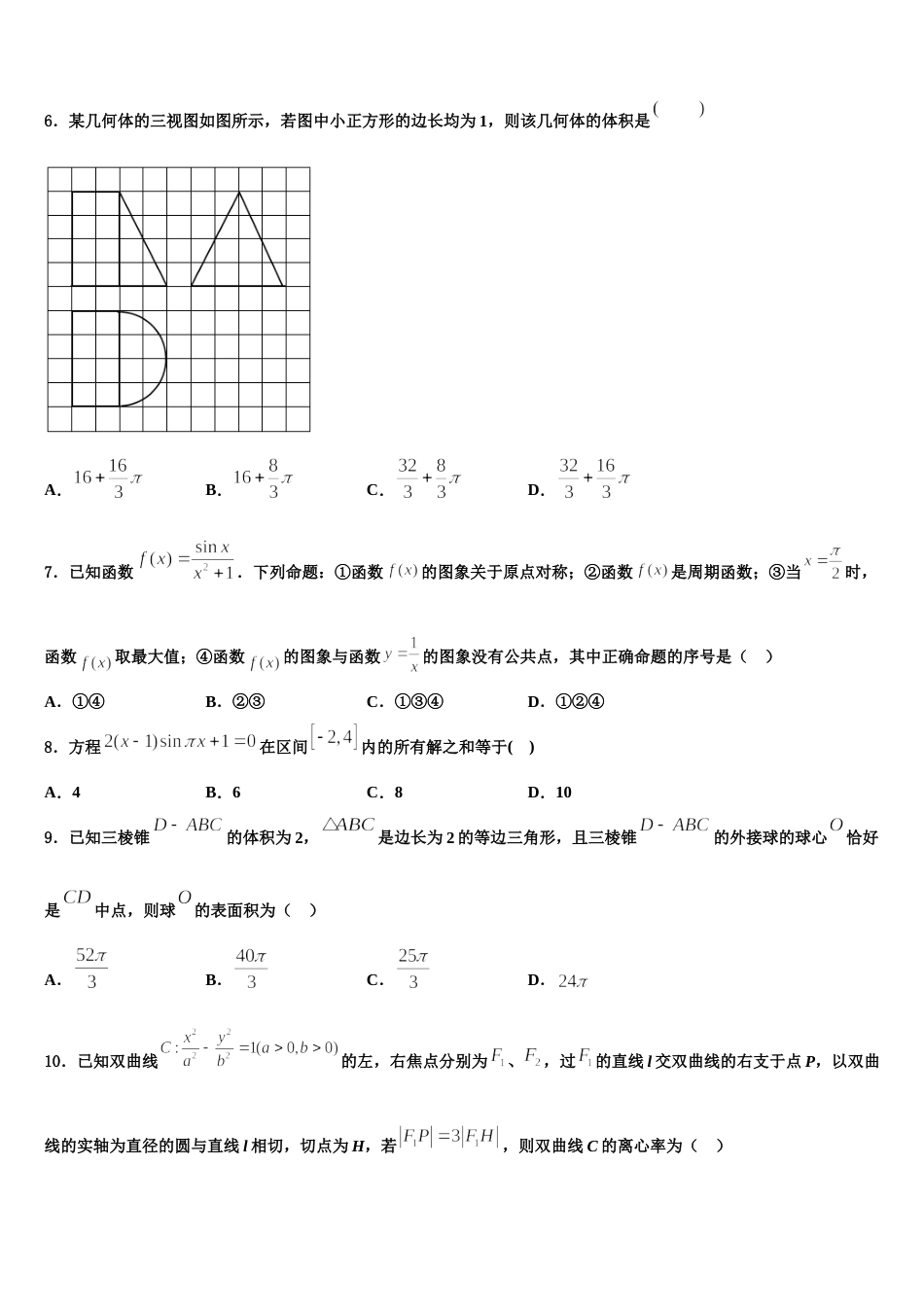
吉林省通化市梅河口市第五中学 2024 年高考全国统考预测密卷数学试卷注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。2.答题时请按要求用笔。3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.若集合,,则( )A.B.C.D.2.单位正方体 ABCD-,黑、白两蚂蚁从点 A 出发沿棱向前爬行,每走完一条棱称为“走完一段”.白蚂蚁爬地的路线是 AA1→A1D1→‥,黑蚂蚁爬行的路线是 AB→BB1→‥,它们都遵循如下规则:所爬行的第 i+2 段与第 i段所在直线必须是异面直线(iN*).设白、黑蚂蚁都走完 2020 段后各自停止在正方体的某个顶点处,这时黑、白两蚂蚁的距离是( )A.1B.C.D.03.若复数满足,则对应的点位于复平面的( )A.第一象限B.第二象限C.第三象限D.第四象限4.下列命题是真命题的是( )A.若平面,,,满足,,则;B.命题:,,则:,;C.“命题为真”是“命题为真”的充分不必要条件;D.命题“若,则”的逆否命题为:“若,则”.5.设,,是非零向量.若,则( )A.B.C.D.6.某几何体的三视图如图所示,若图中小正方形的边长均为 1,则该几何体的体积是 A.B.C.D.7.已知函数.下列命题:①函数的图象关于原点对称;②函数是周期函数;③当时,函数取最大值;④函数的图象与函数的图象没有公共点,其中正确命题的序号是( )A.①④B.②③C.①③④D.①②④8.方程在区间内的所有解之和等于( )A.4B.6C.8D.109.已知三棱锥的体积为 2,是边长为 2 的等边三角形,且三棱锥的外接球的球心恰好是中点,则球的表面积为( )A.B.C.D.10.已知双曲线的左,右焦点分别为、,过的直线 l 交双曲线的右支于点 P,以双曲线的实轴为直径的圆与直线 l 相切,切点为 H,若,则双曲线 C 的离心率为( )A.B.C.D.11.如图所示,网格纸上小正方形的边长为 1,粗线画出的是某几何体的三视图,则该几何体的体积是( )A.B.C.D.812.将函数图象上每一点的横坐标变为原来的 2 倍,再将图像向左平移个单位长度,得到函数的图象,则函数图象的一个对称中心为( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知多项式满足,则_________,__________.14.在的展开式中,所有的奇数次幂项的系数和为-64,则实数的值为__________.15.如图所示,在△ABC 中,AB=AC=2,,,AE 的延长线交 BC 边于点 F,若,则____.16.如图,养殖公司欲在某湖边依托互相垂直的湖岸线、围成一个三角形养殖区.为了便于管理,在线段之间有一观察站点,到直线,的距离分别为 8 百米、1 百米,则观察点到点、 距离之和的最小值为______________百米.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)在直角坐标系中,曲线的参数方程为(为参数,以坐标原点为极点,轴的正半轴为极轴,取相同长度单位建立极坐标系,曲线的极坐标方程为.(1)求曲线的极坐标方程和曲线的普通方程;(2)设射线与曲线交于不同于极点的点,与曲线交于不同于极点的点,求线段的长.18.(12 分)已知函数(1)讨论的单调性;(2)当时,,求 的取值范围.19.(12 分)已知矩形纸片中,,将矩形纸片的右下角沿线段折叠,使矩形的顶点 B落在矩形的边上,记该点为 E,且折痕的两端点 M,N 分别在边上.设,的面积为 S.(1)将 l 表示成 θ 的函数,并确定 θ 的取值范围;(2)求 l 的最小值及此时的值;(3)问当 θ 为何值时,的面积 S 取得最小值?并求出这个最小值.20.(12 分)如图所示的几何体中,,四边形为正方形,四边形为梯形,,,,为中点.(1)证明:;(2)求二面角的余弦值.21....