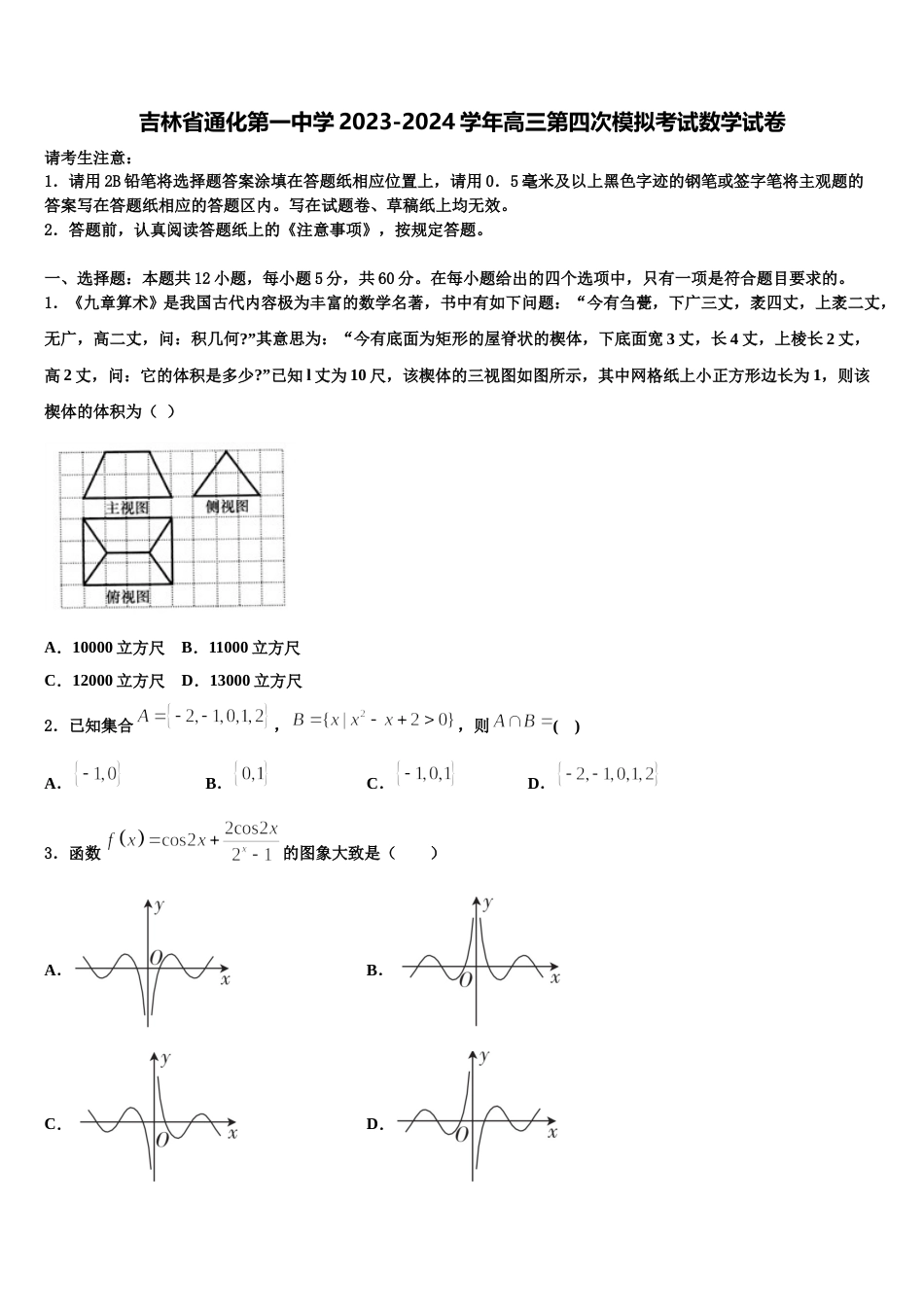
吉林省通化第一中学 2023-2024 学年高三第四次模拟考试数学试卷请考生注意:1.请用 2B 铅笔将选择题答案涂填在答题纸相应位置上,请用 0.5 毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高二丈,问:积几何?”其意思为:“今有底面为矩形的屋脊状的楔体,下底面宽 3 丈,长 4 丈,上棱长 2 丈,高 2 丈,问:它的体积是多少?”已知 l 丈为 10 尺,该楔体的三视图如图所示,其中网格纸上小正方形边长为 1,则该楔体的体积为( )A.10000 立方尺 B.11000 立方尺C.12000 立方尺 D.13000 立方尺2.已知集合,,则( )A.B.C.D.3.函数的图象大致是( )A.B.C.D.4.设某大学的女生体重 y(单位:kg)与身高 x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为=0.85x-85.71,则下列结论中不正确的是A.y 与 x 具有正的线性相关关系B.回归直线过样本点的中心(,)C.若该大学某女生身高增加 1cm,则其体重约增加 0.85kgD.若该大学某女生身高为 170cm,则可断定其体重比为 58.79kg5.若实数 x,y 满足条件,目标函数,则 z 的最大值为( )A.B.1C.2D.06.等比数列的前项和为,若,,,,则( )A.B.C.D.7.设等差数列的前项和为,若,,则( )A.21B.22C.11D.128.如图所示,在平面直角坐标系中,是椭圆的右焦点,直线与椭圆交于,两点,且,则该椭圆的离心率是( )A.B.C.D.9.记等差数列的公差为,前项和为.若,,则( )A.B.C.D.10.如图,在中,点,分别为,的中点,若,,且满足,则等于( )A.2B.C.D.11.党的十九大报告明确提出:在共享经济等领域培育增长点、形成新动能.共享经济是公众将闲置资源通过社会化平台与他人共享,进而获得收入的经济现象.为考察共享经济对企业经济活跃度的影响,在四个不同的企业各取两个部门进行共享经济对比试验,根据四个企业得到的试验数据画出如下四个等高条形图,最能体现共享经济对该部门的发展有显著效果的图形是( )A.B.C.D.12.设等比数列的前项和为,则“”是“”的( )A.充分不必要B.必要不充分C.充要D.既不充分也不必要二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.正四面体的一个顶点是圆柱上底面的圆心,另外三个顶点圆柱下底面的圆周上,记正四面体的体积为,圆柱的体积为,则的值是______.14.已知为椭圆内一定点,经过引一条弦,使此弦被点平分,则此弦所在的直线方程为________________.15.若 x,y 满足,且 y≥−1,则 3x+y 的最大值_____16.直线 是圆:与圆:的公切线,并且 分别与轴正半轴,轴正半轴相交于,两点,则的面积为_________三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知椭圆:过点,过坐标原点作两条互相垂直的射线与椭圆分别交于,两点.(1)证明:当取得最小值时,椭圆的离心率为.(2)若椭圆的焦距为 2,是否存在定圆与直线总相切?若存在,求定圆的方程;若不存在,请说明理由.18.(12 分)某公司打算引进一台设备使用一年,现有甲、乙两种设备可供选择.甲设备每台 10000 元,乙设备每台9000 元.此外设备使用期间还需维修,对于每台设备,一年间三次及三次以内免费维修,三次以外的维修费用均为每次 1000 元.该公司统计了曾使用过的甲、乙各 50 台设备在一年间的维修次数,得到下面的频数分布表,以这两种设备分别在 50 台中的维修次数频率代替维修次数发生的概率.维修次数23456甲设备5103050乙设备05151515(1)设甲、乙两种设备每台购买和一年间维修的花费总额分别为和,求和的分布列;(2)若以数学期望为...