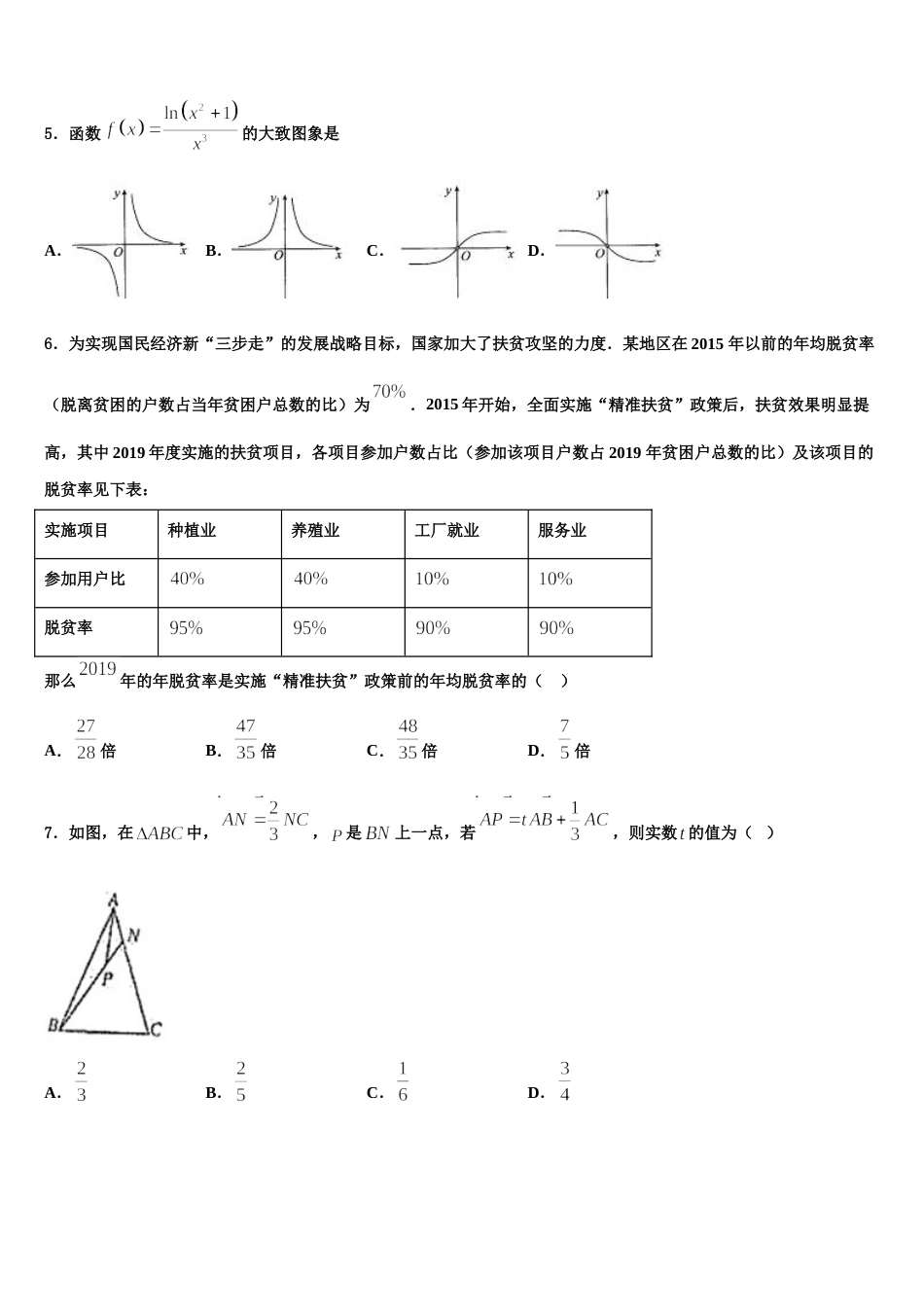
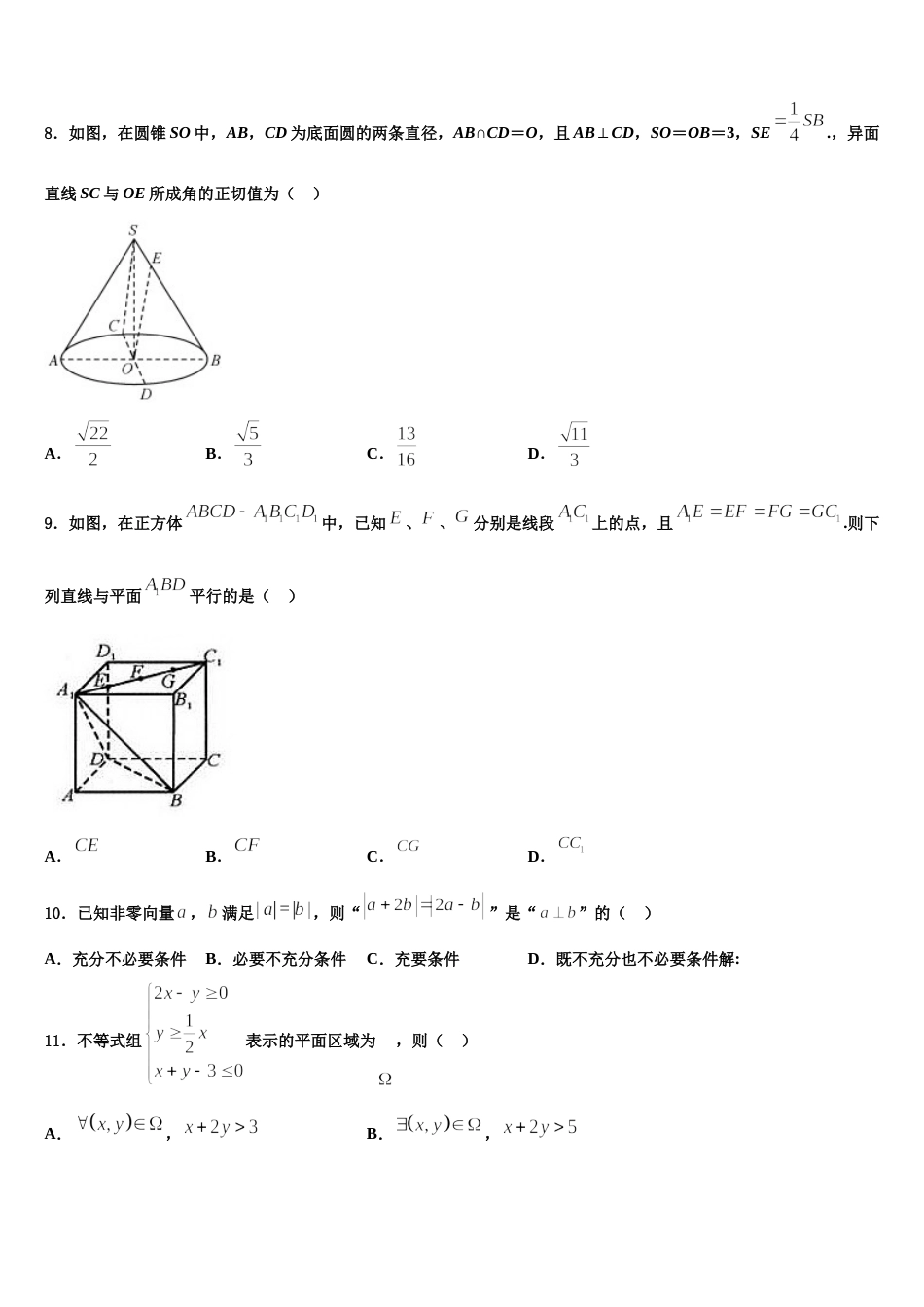
吉林省长春市外国语学校 2024 届高考数学必刷试卷考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用 2B 铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.如图在直角坐标系中,过原点作曲线的切线,切点为,过点分别作、轴的垂线,垂足分别为、,在矩形中随机选取一点,则它在阴影部分的概率为( )A.B.C.D.2.若函数在时取得极值,则( )A.B.C.D.3.已知集合,则集合( )A.B.C.D.4.给出以下四个命题:① 依次首尾相接的四条线段必共面;② 过不在同一条直线上的三点,有且只有一个平面;③ 空间中如果一个角的两边与另一个角的两边分别平行,那么这两个角必相等;④ 垂直于同一直线的两条直线必平行.其中正确命题的个数是( )A.0B.1C.2D.35.函数的大致图象是A.B.C.D.6.为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度.某地区在 2015 年以前的年均脱贫率(脱离贫困的户数占当年贫困户总数的比)为.2015 年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中 2019 年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:实施项目种植业养殖业工厂就业服务业参加用户比脱贫率那么年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )A.倍B.倍C.倍D.倍7.如图,在中,,是上一点,若,则实数 的值为( )A.B.C.D.8.如图,在圆锥 SO 中,AB,CD 为底面圆的两条直径,AB∩CD=O,且 AB⊥CD,SO=OB=3,SE.,异面直线 SC 与 OE 所成角的正切值为( )A.B.C.D.9.如图,在正方体中,已知、、分别是线段上的点,且.则下列直线与平面平行的是( )A.B.C.D.10.已知非零向量,满足,则“”是“”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解:11.不等式组表示的平面区域为,则( )A.,B.,C.,D.,12.已知角的顶点与原点重合,始边与轴的正半轴重合,终边经过点,则( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.曲线在点处的切线方程为______.14.已知平面向量与的夹角为,,,则________.15.某公园划船收费标准如表:某班 16 名同学一起去该公园划船,若每人划船的时间均为 1 小时,每只租船必须坐满,租船最低总费用为______元,租船的总费用共有_____种可能.16.已知函数的最大值为 3,的图象与 y 轴的交点坐标为,其相邻两条对称轴间的距离为 2,则三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知是等腰直角三角形,.分别为的中点,沿将折起,得到如图所示的四棱锥.( )Ⅰ 求证:平面平面.()Ⅱ 当三棱锥的体积取最大值时,求平面与平面所成角的正弦值.18.(12 分)如图,已知椭圆经过点,且离心率,过右焦点且不与坐标轴垂直的直线 与椭圆相交于两点.(1)求椭圆的标准方程;(2)设椭圆的右顶点为,线段的中点为,记直线的斜率分别为,求证:为定值.19.(12 分)已知等差数列中,,数列的前项和.(1)求;(2)若,求的前项和.20.(12 分)已知函数,.(Ⅰ)判断函数在区间上零点的个数,并证明;(Ⅱ)函数在区间上的极值点从小到大分别为,,证明:21.(12 分)表示,中的最大值,如,己知函数,.(1)设,求函数在上的零点个数;(2)试探讨是否存在实数,使得对恒成立?若存在,求的取值范围;若不存在,说明理由.22.(10 分)已知函数.(1)若,证明:当时,;(2)若在只有一个零点,求的值.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、A【解...